1. はじめに
Null という語,データベースに携わっている人なら見たことないという人はいないと思いますが,なんと発音していますか?
「ヌル」って言うのだよ,と誰が教えたのでしょうか?結構,皆さん,ヌル,ヌル,って言っています.違うんですねー.「ナル」って発音するのです.英語の発音記号は nʌ’l です.英語の発音を日本語で書き表すのは難しいですが,決してヌルではありません.英語を母国語とする人にヌルと言ったら,多分首を傾げると思いますよ.ナルって言いましょう.
さて,ナル(null)は「値がない」(having no value)という意味ですね.これに異議ありという方は多分いないと思います.では,リレーショナルデータベースでナルはどのような時にどのように使われているのでしょうか?なんで今さらそんなことを聞いているの?といぶかしげな読者の顔が浮かびますが,ナルに関しては蘊蓄を傾ければきりがなく,理論面でも実践面でも不明確なところが多々あり,議論しだしたらきりがないのかなといった感じです.しばしナル談議に耽ってみたいと思います.
2. NULL とは
2.1 ANSI/X3/SPARC によるナルの顕現
皆さん,ANSI/X3/SPARCはご存じでしょうか?American National Standards Institute/Committee on Computers and Information Processing/Standards Planning And Requirements Committee の略称です.米国国家規格協会(ANSI)の下にあるこの委員会は 1975 年に DBMS の標準アーキテクチャとして名高い「3 層スキーマ構造」を提案した報告書[1]を世に出した団体としてとても有名ですが,その報告書の中で概念スキーマレベルのドメイン関連事項として,ナルの意味は 14 種に上るという報告をしています.このように,ナルはデータベースに係る諸活動の極めて初期から関心が高かったわけです.原義を損ないたくないので,ナルの 14 種の意味を原文のまま引用すると下記の通りです.目を通してみると分かると思いますが,ナルが出現する状況を実にさまざまな観点からピックアップしています.興味を持った方はぜひ一つひとつにあたってみてください.最後の (14)項で,“Derived from null conceptual data (any of the above)”と締め括っているので,トータル 14 種ということです.
Manifestation of null(ナルの顕現)
(1)
| Not valid for this individual (e.g., maiden name of male employee). |
(2)
| Valid, but does not yet exist for this individual (e.g., married name of female unmarried employee). |
(3)
| Exists, but not permitted to be logically stored (e.g., religion of this employee). |
(4)
| Exists, but not knowable for this individual (e.g., last efficiency rating of an employee who worked for another company). |
(5)
| Exists, but not yet logically stored for this individual (e.g., medical history of newly hired employee). |
(6)
| Logically stored, but subsequently logically deleted. |
(7)
| Logically stored, but not yet available. |
(8)
| Available, but undergoing change (may be no longer valid). |
(9)
| Available, but of suspect validity (unreliable). |
(10)
| Available, but invalid. |
(11)
| Secured for this class of conceptual data. |
(12)
| Secured for this individual object. |
(13)
| Secured at this time. |
(14)
| Derived from null conceptual data (any of the above). |
2.2 E.F. Codd によるナルと 3 値論理の導入
では,リレーショナルデータモデルではナルはどのように定義されているのでしょうか?それはリレーショナルデータモデルの始祖コッド(Edgar F. Codd)の 1979 年の論文[2]に見ることができます.そこでは,ナルとナル値(null value)という用語が出現しますが,それらは次のように与えられています.
まず,主キーの値はナルであってはいけないというルールの提唱があります.これはキー制約として知られていることで,もっともなことです.続いて,ナル値の最も重要なタイプは 2 つあって,それらは “value at present unknown”(値は現時点で未知)と“property inapplicable”(不適当なプロパティ)という意味を持つと述べています.そのうえで,ナル値を許すとリレーショナル代数を拡張しなければならないが,拡張のためには前者の “value at present unknown” に関心があるとし,それを “ω” で表して,いわゆる 3 値論理を展開しました.
本稿は,コッドは「ナル」をどう捉えたのかに焦点を当てて議論することが狙いなので 3 値論理や
一般に多値論理の議論には深入りしませんが,リレーショナル代数を 3 値論理に拡張するにあたり,
value at present unknown,すなわちナル(ω)を許したときに,リレーショナル代数を構成する 8 つの演算,つまり 4 つの集合演算(和,差,共通,直積)とリレーショナル代数に特有な 4 つの演算(射影,選択,結合,商)をどのように定義し直すべきかという問題だけは復習しておきたいと思います.これについて,まず,4 つの集合演算と射影は集合意味論のもとで素直に拡張できます.問題は,選択演算です.選択演算での “ω” の扱いが決まれば,結合は直積と選択,商は直積と射影と差を用いて定義できるので特段の問題は生じません.そこで,属性が ω をとる場合に選択演算がどのように拡張されることになるのか,それを見てみましょう.
そこで,値式 x, y に対して,述語 xθy,ここに θ は比較演算子(=,<,≦,>,≧,≠),がどのような真理値をとるかを見ていきます.従来のリレーショナルデータモデルの 2 値論理の場合と同じく,x と y が共にナルでなければそれは真(true,T)か偽(false,F)をとります.では x または y ,あるいはその両方がナルとなる場合,述語 xθy はどのような真理値をとるのでしょうか?これに対してコッドは,不定(unknown)をとるとしました.そして,述語 xθy の真理値表(3 値論理)を表 1 に示したように定義しました.表示されているように,コッドは,ω を「値は現時点で未知」を表すだけでなく「不定」という真理値を表すためにも使用しました.こうすることで,「不定」という真理値をデータベースに格納することができ,かつすべての「不定」や「値は現時点で未知」の処理を統一的に行えるとしました.
表 1 述語 xθy の真理値表(3 値論理)

x, y は現実値(real value).θ は比較演算子
では,真(T)か偽(F)か不定(ω)をとる 3 値論理はどのような真理値表を有するのでしょうか?それが表 2 に示される 3 値論理の真理値表(NOT ブール演算子のための真理値表,AND ブー
ル演算子のための真理値表,OR ブール演算子のための真理値表)です.一般に 3 値論理の定義は
ただ一つというわけではありませんが,表 2 で与えられた定義はクリーネ(S. C. Kleene)の 3 値
論理の真理値表と同一となっています.
表 2 3 値論理の真理値表[2]
![3 値論理の真理値表[2]](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/10/drmasunaga-09-P03-02.png)
以上の結果を使うと,NOT,AND,OR で結合された一般的な述語の真理値を求めることができます.たとえば, 5≦2 OR 5=ω の真理値は,述語 5≦2 の真理値が F,述語 5=ω の真理値が ω なので,OR ブール演算子のための真理値表を見ることで,5≦2 OR 5=ω の真理値は ω であることが分
かります.
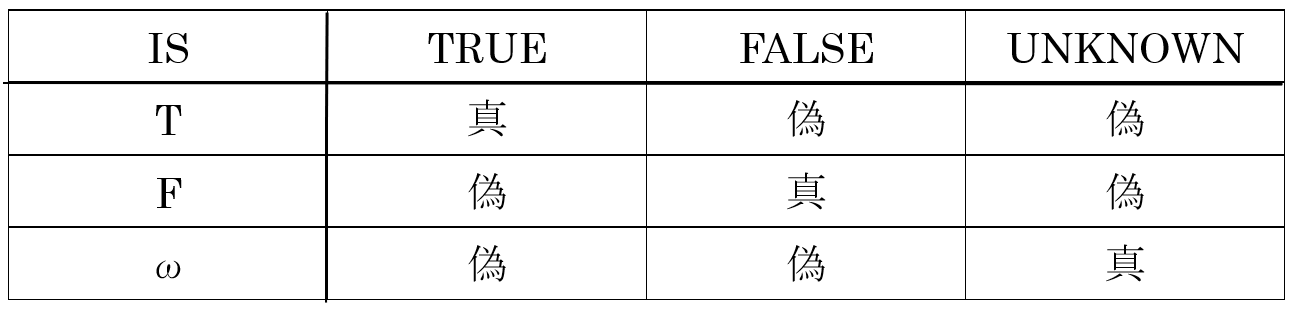
そうすると,表 3 に示す IS ブール演算子真理値表を定義することができ,それにより探索条件が TRUE であるのか,FALSE であるのか,UNKNOWN であるのかを決定することが可能となります.
たとえば,5≦2 OR 5=ω IS UNKNOWN という述語,すなわち探索条件,の真理値は 5≦2 AND 5=ω
の真理値が ω なので真であるという具合です.
表 3 IS ブール演算子真理値表(3 値論理)
以上の枠組みのもとで,コッドは従来のリレーショナルデータモデルが依って立つ 2 値論理のと
きの θ -選択演算や θ -結合演算の自然な拡張として,3 値論理のための推量 θ-選択演算(maybe θ-selection operation)と推量 θ-結合演算(maybe θ-join operation)を定義しました(従来の
演算は推量演算と区別するために真正(true)という接頭辞を付けられて区別されます).ここに,
maybe(推量)は「真理値が真でもなく偽でもなく,おそらく真でありおそらく偽であるのだが,
DBMS はどちらが成立するのかは知らない」を意味します.推量 θ -選択演算の定義は次の通りで
す.なお,推量 θ -結合演算の定義は直積と推量θ-選択演算の定義を使って与えることができますが,詳細に関心のある者は文献[2]や拙著[3]を参照してください.
【定義1】(推量 θ -選択演算)
R(A1, A2, …, An) をリレーションとする.Ai と Aj を θ-比較可能とするとき,R の属性 Ai と Aj 上の推量 θ-選択,これを R[Aiθω Aj] と表す,は次にように定義されるリレーションである.
R[Aiθω Aj]={t|t∈R∧t[Ai]θt[Aj] IS UNKNOWN}
【例題1】(推量 θ -選択演算)
リレーション R(A, B, C)={(1, 5, 3), (2, 3, 8), (3, 2, null), (4, null, 6), (5, null, null)} としたときの,
R の B,C 上の真正大なり -選択 R[B>C] と推量大なり -選択 R[B>ωC] の結果は次のようになる.
R[B>ωC]の結果が下記のようになることは,5>3=真(T),3>8=偽(F),2>null=不定(ω),
null>6=不定(ω),null>null=不定(ω)であるので,2>null,null>6,null>null の場合
でのみ t[B] θ t[C] IS UNKNOW が真となることから分かる.
R[B>C]={(1, 5, 3)}
R[B>ωC]={(3, 2, null), (4, null,6), (5, null, null)}
なお,この 3 値論理の議論で興味深いことは,コッドが value at present unknown を表す ω は
いつでも非ナル値(nonnull value)をとれるプレースホルダ(placeholder)と考えるのがよいだ
ろうとも述べていることです.ナルはあくまでナルであってナル値という概念はないのだよと日頃
から言っている筆者にとっては,ここが大変微妙に感じられるところです.つまり,ω はナル値だ
と言いながら一方でプレースホルダ,つまり値ではなく単なる「標識」だと言っているわけで,
コッドがオックスフォード大学の数学科出身であることを考えるとき,数学的厳密さからは,
彼自身,「ナルは値なの?そうではないの?」と,この相反する概念規定にいささかの葛藤が
あったのではないか,と想像するわけです.
2.3 E.F. Codd によるナルと 4 値論理の導入
3 値論理の導入後,コッドはナルの意味をより豊富に捉えて,それをリレーショナル DBMS は
サポートするべきであるとし,4 値論理を提案[4, 5]したことはよく知られている通りです.ただ,
4 値論理の議論は時期尚早としてそれ以上の議論は行いませんでしたが,そこでは,真理値として,
t (true),i (missing and inapplicable),a (missing and applicable),f (false)の 4 つを導入し,
表 4 に示される 4 値論理の真理値表を与えています[5].
表 4 4 値論理の真理値表
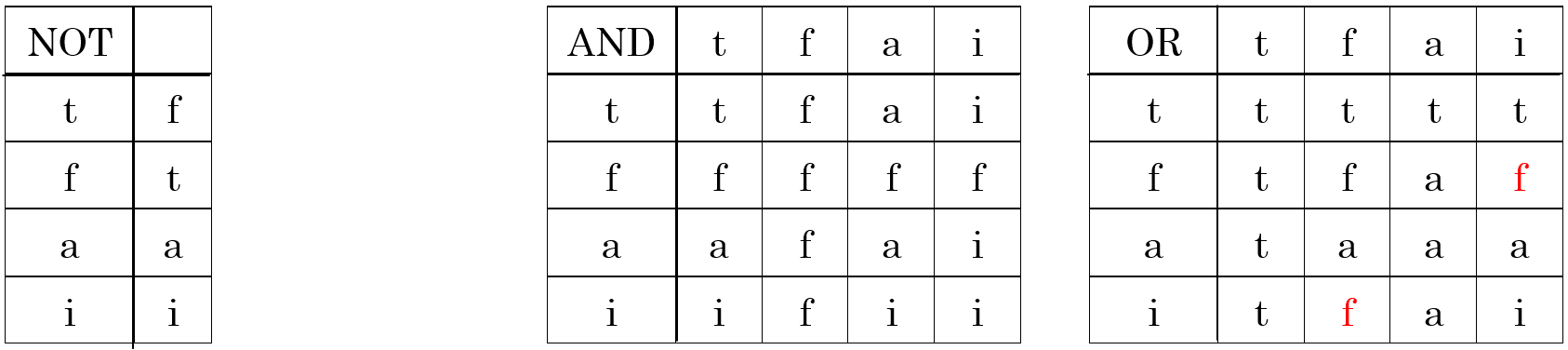
この真理値表は一見すると表 2 に示した T,F,ω を擁する3値論理の真理値表の素直な拡張になっているように見えますが,注意深く見てみると OR ブール演算子のための真理値表の f 行 i 列,つまり f OR i の真理値が i ではなく f となっています(対称的に,i 行 f 列,つまり i OR f についても同様です).このことについて,論文[5]に 4 値論理の真理値表を表 4 のように定義した論拠は一切示されていないのでその理由を知ることはできませんが,この真理値表の直下に,次のような注意書きを与えています(原義を損なわないために原文のママ引用します ).
|
“Note that we obtain the truth table of the TRI/EFC-4 three-valued logic by replacing i by m and a by m (where m simply stands for missing, and the reason for anything being missing is ignored).” |
TRI/EFC-4 とはコッドが立ち上げた研究機関 The Relational Institute (TRI) で E.F. Codd (EFC) が
書いた 4 番目の論文 “Missing Information in Relational Databases: Applicable and Inapplicable”, February 21, 1986 を指しています.コッドはこの注意書きで,i と a を共に m に置き換えると,
表 2 に示した 3 値論理の真理値表が得られるというのですが,実際それを行ってみると,3 値論
理の NOT ブール演算子のための真理値表と AND ブール演算子のための真理値表は得られますが,
OR ブール演算子のための真理値表は得られません(読者の皆さんも容易に確かめることができる
と思います).OR ブール演算子のための真理値表が i と a を共に m に置き換えることで得られる
ためには,f 行 i 列,つまり f OR i の真理値は f ではなく i でないといけません(対称的に,i 行
f 列,つまり i OR f についても同様です).ただ,一般に多値論理の定義には多様性があり,たと
えばベルナップ(Nuel D. Belnap, Jr.)の定義した 4 値論理 A4 や L4 の真理値表はコッドの定義
した真理値表(表 4)とは異なります. 筆者は「i と a を共に m に置き換えると,云々」という
箇所にこだわり,表 4 に疑問符を投げかけましたが,それにこだわらなければ表 4 でよいのかも
しれません.コッドが没してしまった今となっては,本人にその真意を問うことはできませんが,
もし 4 値論理をリレーショナルデータベースに実装しようとするのであれば,解決を迫られる避け
ては通れない問題だろうと考えられます.
2.4 SQL でのナル
国際標準リレーショナルデータベース言語 SQL でのナルに対する立ち位置はどのようでしょうか?メルトン(J. Melton)らの著書[6]に次のような説明があります.ちなみに,メルトンは SQL-92 や SQL:1999 の編集者(editor)で,SQL の策定に多大な影響力を持っている人として知られています.ここで述べるナルに対する SQL のスタンスは最新規格SQL:2016[7]でも変わっていません.
|
『SQL ではデータ項目が現実値(real value)を持たない場合にフラグのようなもの (a sort of flag)を格納します.そして,現実値が提供されていないことを示す フラグが設定されているとき,そのデータ項目はナル値を持つといいます』 |
若干補足すると,SQL ではデータ項目は非ナル値(non-null value)かナル値をとります.ナル値
は “not available”(入手不可),“not applicable”(適用不可),“unknown”(未知)を表すために使用
され,キーワード NULL を導入してナル値を表します.ナル値はいかなるデータ型の値でもないので,
もし NULL にあるデータ型を関連付けたいのであれば CAST(NULL AS datatype) 句で明示的にデータ
型と関連付けます.
つまり,SQL ではデータ項目が現実値を持たないことを NULL で表すとしているわけですが,それをナル値と言ってしまったので,あたかもナルという値があるかのような表現になっています.したがって,ここでもコッドが直面したであろう葛藤が読み取れて,現実値がないのにあたかも「ナルという値」があるかのように言ってしまう...この可笑しさについては SQL を策定した当事者自身もどうも気にしていたようで,メルトンらは上記の著書[6]で次のように釈明しています.言うまでもありませんが,this phrase とは上記の説明文のことです.
|
“This phrase is probably a misleading, because null means that there is no “real” value at all; nevertheless, it’s a convenient shorthand that you will often find in use.” |
こんな釈明をするぐらいならば,次のような一貫した姿勢をとった方がどれだけすっきりした体系となっただろうにと,筆者は常々思うわけです.
| 『値がないことを NULL で表す.あくまで NULL は標識であって,ナル値という概念はない』 |
3. ナルの意味の体系化
前章で示したごとく,ANSI/X3/SPARC はナルに対して 14 種の意味を,コッドはナル値に “value
at present unknown” と “property inapplicable” という 2 つの意味を,SQL はナルに “not available”
(入手不可),“not applicable”(適用不可),“unknown”(未知)という 3 つの意味を与えています.
問題は,それぞれがそれぞれの思惑からナル(値)の定義を与えていますが,データベースでナルを中途半端ではなくきちんと取り扱うためには,ナルの意味の健全かつ完全な体系化が必要となります.ここに,健全(sound)であるとは,その体系において構文論的に証明できる命題は意味論的に成り立つことをいい,完全(complete)であるとは意味論的に成り立つ命題は構文論的に証明できることを
意味します.以下で議論するように,この意味で,ANSI/X3/SPARC,コッド,そして SQL のナルの
取り扱いは不十分だということです.
3.1 コッドによるナルの意味の体系
さて,コッドが 4 値論理の議論で与えたナルの分類が完全なように見えるかもしれません.しかし,以下に示すようにそうではありません.コッドは,ナル値の最も重要なタイプは 2 つあって,それら
は value at present unknown と property inapplicable であり,それに基づき,値がない場合,つま
り missing の場合を missing and applicable と missing and inapplicable の 2 つに分類しました.
Applicable と inapplicable で二律背反ですから,この分類に限れば完全です.しかしながら,コッド
の分類で問題があると考えられるところは,そもそも値があるのかないのか,それが分からないとい
う理由で missing の場合がフォーマライズされていないことです.確かに,コッドの論文[4]を丁寧に
見ると,そこに掲載されている Fig.1 で missing values を分類して,applicable と inapplicable に
加えて other という枝分かれを確認することができます(その結果,missing values は 3 種類という
ことになります).この other ですが,本文中に説明は見当たらず,Fig.1 中に記載があるだけなの
ですが,その図を拠り所にしてコッドが考えた missing value の概念を分類木(classification tree)
で表してみると図 1 のように描けます.しかし,other がこのような位置づけでは,3.3 節の議論で
明らかになるように,ナルの健全かつ完全な分類とはなっていないのです.
![コッドのmissing values[4]の分類木](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/10/drmasunaga-09-P08-01.png)
図 1 コッドの missing values[4]の分類木
3.2 SQL によるナルの意味の体系
SQL は,2.4 節で述べた通り,ナル値には次の3つがあるとしています[6].

“not available” は何らかの理由で属性値が入手不可,“not applicable” はこのタップルがその属性で現実値をとることはありえず適用不可,“unknown” は属性値は存在するはずだが未知,を表しています.この分類ですが,コッドが与えた “missing and applicable”,“missing and inapplicable”,“other” という 3 分類とは異なるようです.個人的な感覚レベルでは,“not applicable” と “missing and inapplicable” が対応しているのだろうとは思いますが,他は漠然としていてよく分かりません.多分,対応付けしようとする方がおかしいのだろうと思います.SQL のナルの分類は属性が現実値をとれないと考えられる場合を3つピックアップしただけという感じで,場当たり的な分類の感はぬぐえず,ナルの健全かつ完全な分類からは遠い気がします.
なお,SQL はナル値には 3 つの意味があるとはしましたが,一律に NULL で表してしまうので,意味の違いを表現することはできません.
3.3 SQL ナルの意味の健全かつ完全な体系化
ナルの意味の体系化に対して何かすっきりした解決策はないものかと思案していたとき,かつて筆者の目に留まったのが,ナルの持つ「3 つの意味」に着目してそれを分類する考え方です[8].ここに,ナルの持つ3つの意味とは次のとおりです.

このナルの意味付けは,対象とした属性がとりうる値の存在の有無に視点を置き,その可能性を分類すると,次に示す 4 つの場合になることに理論的根拠を置いています.

確かに,属性値の存在を問うたときに,属性値が存在する,属性値が存在しない,属性値が存在するのかしないのか分からない,この 3 つに分類されますね,と言われればその通りです.さらに,属性値が存在するとしても,現時点で分かっている場合もあれば,分かっていない場合もありますね,と言われればそれも確かにその通りです.この分類則を分類木で表してみると図 2 のようになります.この分類木の作り方から,属性値の存在に関してこの分類が健全かつ完全であることはほぼ明らかでしょう.
![コッドのmissing values[4]の分類木](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/10/drmasunaga-09-P09-03.png)
図 2 ナルの持つ「3つの意味」に着目した分類木
補足ですが,この分類の下で,現実値,unk, dne, ni の違いをそれらが担っている情報量の違いで
説明することができます.つまり,ナルを受け取る側からみると,ni は unk や dne に比べて情報量
が少なく(less informative),unk は現実値が与えられることに比べれば情報量は少ないと言えま
す.また,現実値と dne の情報量の多寡は less informative とも more informative とも言えないでしょう.同様なことが異なる 2 つの現実値同士についても言えると考えられます.したがって,現実
値を di(i=1, 2, …, n)とするとき,集合 {d1, d2, …, dn, unk, dne, ni} は情報量の多寡を半順序関係(partial order relation)とする下半束(lower semilattice)をなしていると表現することができます.その様子を図 3 に示します.
![コッドのmissing values[4]の分類木](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/10/drmasunaga-09-P10-01.png)
図 3 ナルの持つ「3つの意味」のなす下半束[8]
【例題2】(unk,dne,ni の具体例)
リレーション 社員(社員名_姓,社員名_名,配偶者名) を想定する.
- unk の例:社員の属性として配偶者名があるとき,配偶者がいることは分かっているのだが,現時点でその名が分からないとき配偶者名欄に unk を記入する.
- dne の例:社員の属性として配偶者名があるとき,配偶者がいない社員の配偶者名欄に dne を記入する.
- ni の例:社員の属性として配偶者名があるとき,配偶者がいるのかいないのか分からない社員の配偶者名欄に ni を記入する.
ただし,次の注意が必要です.たしかに,上記の分類でナルの意味は過不足なく表現することができました.しかしながら,これは言わずもがなですが,もし unk,dne,ni すべてを一律に null で表してしまうとこの分類体系は無意味になってしまいます.たとえば,リレーション社員(社員名_姓,社員名_名,配偶者名)にタップル(鈴木,太郎,null)が存在した場合,null が unk を表しているのか,dne を表しているのか,あるいは ni を表しているのかは分からないということです.このようなことにならないためには,リレーショナル DBMS は unk,dne,ni をいかなるドメインにも属さない特別なプレースホルダとして扱える機能を備えていないといけないということになります.ただ,これも言わずもがなですが,現行のプロプライエタリあるいは OSS のリレーショナル DBMS に unk,dne,ni を個別にサポートするような機能は備わっていません.これは,SQL が not available,not applicable,
unknown を一律に NULL と表し処理していることと同じです.
4.NULL と空文字列
ナルとは別に空文字列(zero-length string, ZLS,”で表す)という概念があります.これは長さが 0 の文字列を「値」として持つということで,ナルとは異なります.相違点は,理論上,ナルはいかなるドメインの元ではありませんが,空文字列はすべてのドメインの元であるということです.
さて,空文字列の意味ですが,どう考えたらよいのでしょうか?たとえば,リレーション 友人(氏名,住所,携帯電話番号)があり,タップル (鈴木太郎,横浜,” )があったとします.これは,もしタッ
プルが(鈴木太郎,横浜,null)であった場合と何がどう違うのでしょうか,それを説明してほしいという問題です.もちろん,SQL で問合せを書き下すにあたって,空文字列と null ではその取扱いに違いのあることは十分に承知してのことです.つまり,ここでの関心事は意味の違いです.繰り返しますが,(鈴木太郎,横浜,” )と(鈴木太郎,横浜,null)では一体何がどのように違うのでしょうか?
もし,空文字列(”)で鈴木太郎が携帯電話を持っていないということを表したいというのであれば,携帯電話番号欄は null,正確には dne でしょう.もし,持っているのは分かっているのだけれど
その番号が分からないというのであれば null,正確には unk でしょう.もし持っているのかいないの
か分からないのでということであれば null,正確には ni を記録するべきであって,空文字列ではないでしょう.そうすると,唯一考えられるのは,鈴木太郎の携帯番号が現実値として空文字列(”)であるということになってしまいますが,こんな携帯電話の番号ってありますか?マジ理解に苦しむ世界に落ち込んでしまいました...
『データベースは色即是空空即是色の世界観のもとで成り立っている』
ということでしょうか,奥深いことです.
5.PostgreSQL と NULL および空文字列
OSS のリレーショナルDBMSとして普及している PostgreSQL では用語集(glossary)でナルを次のように定義しています[9].
『Null-リレーショナルデータベース理論の中心的な信条である non-existence
(存在しない)という概念.明確な値がないことを表します』
「明確な値がないことを表します」,原文では “It represents the absence of a definite value.” と書かれているわけですが「明確な値がない」とはどういうことか,ナルはナル値という “値”(value)であるのか単なる標識なのか,それについてはなにも言及されていません.なお,空文字列については特段の定義が与えられているわけではありません.
そこで,念のため,null や空文字列が PostgreSQL で一体どのようにサポートされているのか,
PostgreSQL 14 で検証しつつ気が付いたところを記してみたいと思います.
【検証】(PostgreSQL 14 での NULL と空文字列の扱い)
テーブル test(name char(10), spouse char(10)) を作成し,タップル (‘taro’, ‘hanako’), (‘jiro’, ”), (‘saburo’, null) を挿入して,SQL で空文字列 ” とナル値を表すキーワード null に関する問合せを発行して,PostgreSQL 14 はどのように振舞うのか,その結果を見てみます.なお,PostgreSQL の問合せでのナル値と空文字列の概念の違いはモムジャン(B. Momjian)の著書[10]で平易に説明されているので参考になるかもしれません.

・ 検証事項1
上記の select 文の結果ですが,jiro の spouse(配偶者)値は空文字列 ” のはずですが,空白として表示されています.空文字列だからそうなのでしょう.一方,saburo の spouse 欄は 空文字列ではなく null のはずですが,これまた空白です.したがって,この問合せの結果からは,ユーザは jiro のタップルの spouse 値が空文字列 ” でsaburo のタップルの spouse 欄は null であることを知ることはできません.筆者としては,この問合せに対する導出表は(2)式のように表示されるべきだと思います.導出表をなぜ(2)式のように表示してくれないのでしょか?筆者には謎です.

・ 検証事項2
上記の結果を受けて以下の 2 つの問合せを発行してみます.

この問合せの結果から,spouse 値が空文字列のタップルは jiro のタップルであることが分かります.つまり,空文字列を PostgreSQL は内部的にはちゃんと認識し,述語「 ” = ” 」は T(真)(表 1 述語 xθy の真理値(3 値論理))と認識しています.
一方,次を発行してみます.

この問合せの結果から,spouse 欄が null のタップルは saburo のタップルであること,すなわち,null is null=T(真)(表 3 IS ブール演算子真理値表(3 値論理))と PostgreSQL はちゃんと認識しています.
(3)と(4)から分かるように,PostgreSQL は問合せの結果(1)からはユーザには見えませんでしたが,内部的には空文字列と null をきちんと認識しているわけです.決してごっちゃになっているわけではありません
・ 検証事項3
ここでは,理論上,「spouse is null」は許されたが「spouse is ”」は許されないこと,および「spouse = null」の処理を念のために検証することにします.
まず,「spouse is ”」 は許されないことは次のように確認されます.is true, is null, is false は IS ブール演算子として許されるが,is ” は IS ブール演算子として許されていないので納得です.

では,「spouse = null」はどうでしょうか?

導出表は 0 行という表示ですから,リレーション test には探索条件 spouse = null にヒットするタップルがなかったというわけです.この問合せ処理にあたっては,探索条件 spouse = null に対して,具体的には 3 つの述語 ‘hanako’=null,”=null,null=null を検証しないといけないわけですが
(= は比較演算子),表 1 に示した「述語 xθy の真理値(3 値論理)」から,’hanako’=null の真
理値は ω,”=null の真理値も( ” が空文字列という現実値なので)その真理値は ω,null=null の
真理値も ω ということで,いずれも真(T)ではないので,ヒットした行はなかったということです.
なお,(‘saburo’, null)∈test なので,’saburo’ が導出表に現れるかと思うかもしれませんが,そのためには “spouse=null” ではなく,“spouse is null” を指定しなさいということです(検証事項 2).
・ 検証事項4
update 文では set 句で spouse=null という表現が許されますが,この場合は述語ではなく「代入」を表し,その簡単な例は次の通りです.ただ,更新結果を確認するためにselect文を発行しても,検証事項1でクレームしたと同様に,導出表からは,taro の spouse が空文字列(”)と更新されたのか,
null と更新されたのかを読み解くことはできません.

なお,null や空文字列の扱いはプロプライエタリや OSS のリレーショナル DBMS ごとに異なっているようです.上で見たように PostgreSQL ではそれらを区別して扱っていましたが,Oracle Database では自動的に空文字列を null に変換するとの記事をよく見かけます.空文字列とナルの違いを意識したユースケースを Oracle Database は想定していないということなのでしょう.
6.おわりに
ナル(null)に係わる話題をいくつか披露いたしました.ナルの意味の健全かつ完全な体系化には,属性は「現実値」に加えて,3 種類の意味の異なるナル,すなわち,unk(未知),ni(情報がない),dne(存在しない),をサポートする必要があることを論じました.そのためには,リレーショナルデータモデルとリレーショナル DBMS は 3 値論理を超える多値論理をモデル化し実装していくことが必要になりますが,一筋縄ではいかない難問と考えられます.機会があれば論じてみたいですね.
繰り返すまでもありませんが,本稿をお読みいただいた方々,これをご縁に以下のことお約束ください.
● ヌルとは言わない,必ずナルと言う.
● ナル値とか空値とは言わない,必ずナルあるいは空と言う.
【文献】
[1]
|
ANSI/X3/SPARC Study Group on Data Base Management Systems, Interim Report, ANSI, February 1975, pp. IV-28~IV-29. https://dl.acm.org/action/showFmPdf?doi=10.1145%2F984332 |
[2]
| Edgar. F. Codd. Extending the Database Relational Model to Capture More Meaning. ACM TODS, Vol.4, No.4, pp.397-434, 1979 |
[3]
| 増永良文.リレーショナルデータベース入門[第3版].サイエンス社,2017. |
[4]
| Edgar. F. Codd. Missing Information (Applicable and Inapplicable) In Relational Databases”, ACM Sigmod Record, Vol 15, No. 4, pp.53-78, December 1986. |
[5]
| Edgar. F. Codd. More Commentary on Missing Information in Relational Databases (Applicable and Inapplicable Information). ACM Sigmod Record, Vol 16, No. 1, pp.42-50, March 1987. |
[6]
| Jim Melton and Alan R. Simon. SQL: 1999 : Understanding Relational Language Components. Morgan Kaufmann Publishers, 2002. |
[7]
| Information technology — Database languages — SQL — Part 2: Foundation (SQL/Foundation), Reference number ISO/IEC 9075-2:2016(E), ISO/IEC, 2016-12-15. |
[8]
| Mark A. Roth, Henry F. Korth and Abraham Silberschatz. Null Values in Nested Relational Databases. Acta Informatica 26, pp.615-642, 1989. |
[9]
|
The PostgreSQL Global Development Group. PostgreSQL 14.2 Documentation. https://www.postgresql.org/files/documentation/pdf/14/postgresql-14-A4.pdf |
[10]
| ブルース・モムジャン(著),日本ポストグレスユーザー会(翻訳).はじめてのPostgreSQL データベース問い合わせのコンセプト.ピアソン・エデュケーション,2001. |