1. はじめに
リレーショナル DBMS において質問処理の最適化はリレーショナル DBMS の開発が始まって以来,設計者が最も腐心するところでした.その嚆矢は 1970 年代に IBM San Jose 研究所で開発された System R で提案・実装されたコストベース(cost based approach)の最適化手法です[1].System
R は PostgreSQL の前身である INGRES と共にリレーショナル DBMS のプロトタイプとして名高い
システムですが,そこで開発されたこの手法は現在もプロプライエタリや PostgreSQL を含む OSS
のリレーショナル DBMS の質問処理最適化技法の基本となっています.
この手法は問合せの実行プランを策定するにあたり,問合せ最適化器(query optimizer, 単にオプティマイザ,あるいはプランナ)は,まず単一のリレーションについてコスト最小のアクセスプランを推定し,つぎに,その結果を使って 2 つのリレーションを結合する場合のコスト最小プランを推定し,さらに,3 つのリレーションの結合コストをコスト最小と推定された 2 つのリレーションの結合を使って推定していくので,動的計画法(dynamic programming, DP)の一つとも位置付けられています.
さて,人工知能の一分野である機械学習はさまざまな分野で取り入れられていますが,データベース分野も例外ではありません.データベース分野での機械学習の適用を考えてみると,まずはデータ活用への機械学習の適用でしょう.これに対しては,Oracle Database に一日の長の感があり,「Oracle Database で高性能の機械学習モデルを構築する」といったウェブページが立ち上がっています.データサイエンティストへの支援です( https://www.oracle.com/jp/artificial-intelligence/database-machine-learning/ ).
もう一つは機械学習をオプティマイザに適用する研究・開発でしょう.PostgreSQL には早くからその動きがあり,PostgreSQL 6.1(1997 年 6 月リリース)で GEQO のサポートが始まり現在に至っています.GEQO はユーティッシュ(M. Utesch)[2]の考案により実装されましたが,GEQO はその名前の由来が GEnetic Query Optimization にあることから分かるように,遺伝的アルゴリズム(genetic algorithm, GA)を用いた結合質問処理最適化のための手法です.PostgreSQL に対する問合せ処理最適化への機械学習の適用を見てみると,PostgreSQL の世界会議である PGCon 2007 で Kovarik ら[3]が機械学習と質問処理最適化を論じています.PGCon 2010 では Urbański[4]が結合質問処理の最適化について GEQO に代わる手法として「焼きなまし法」(simulated annealing)を用いた提案をしています.また,PGCon 2017 では Ivanov[5]が Postgres Pro Enterprise の拡張機能として AQO (adaptive query optimization) を報告しています.AQO はコストベースの問合せ最適化のために,機械学習の手法として知られている「k-近傍法」を使用してカーディナリティ推定を改善することで実行計画を最適化しているとのことで,PostgreSQL 9.6 以降で稼働するとのことです.ここに,カーディナリティ推定とはサブプラン作成のために中間結果のリレーションのサイズを推定することをいい,強力なオプティマイザ設計のために欠かせない技術です.PGCon 以外では,オートマトン理論を基にして結合質問処理の最適化を行い GEQO と比較検証した結果が報告されています[6].
また,機械学習で注目を集めている深層学習(deep learning)を質問処理の最適化に適用しようとする研究も報告されており,そこでは PostgreSQL が性能評価のために使用されています[7].
本稿では GA をいち早く質問処理の最適化に導入した GEQO に着目をして,その基本的考え方やその効果を見てみたいと思います.
2. 遺伝的アルゴリズム(GA)とは
GEQO を理解するにあたって,遺伝的アルゴリズム(GA)を理解しておくことが大前提となるので,その説明から始めます.
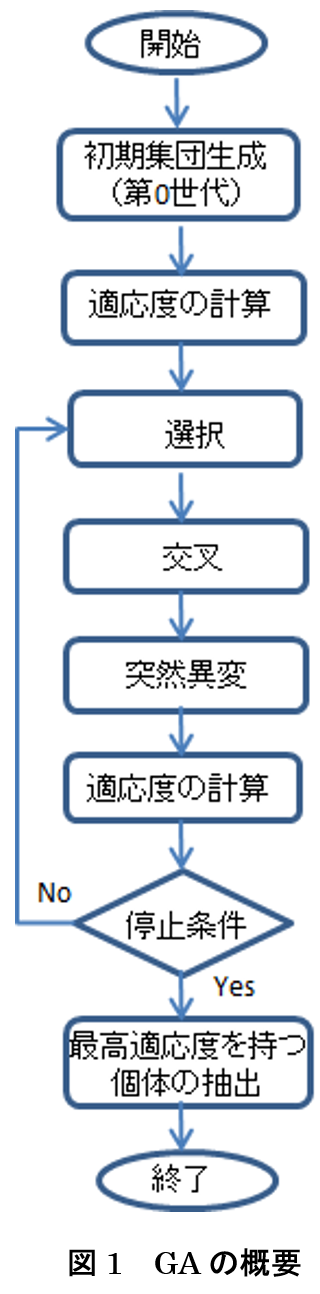
GA は 1975 年にミシガン大学のホーランド(J. H. Holland)により提案されました[8].GA をフローチャートで図 1 に示します[9].このアルゴリズムの概略は次の通りです.
【GA のアルゴリズム】
ステップ1.
| 初期集団(=初期個体群)を用意する(第 0 世代). |
ステップ2.
|
各個体について「適応度」(fitness),つまり,個体が 環境に適応して子孫を残すことのできる能力の度合い, を計算する. |
ステップ3.
|
選択をする.選択とは「両親」(parents)の選択を 意味する. |
ステップ4.
| 遺伝子の交叉(crossover)を起こさせる. |
ステップ5.
| 遺伝子の突然異変(mutation)を起こさせる. |
ステップ6.
| 各個体について適応度を計算する. |
ステップ7.
|
停止条件を満たすか否かを検証する.もし満たしていな ければ,ステップ 3 に行く.満たしていれば,最も高い 適応値を持つ個体を選択して終了する. |
いくつか補足すると次の通りです.
●
| 初期集団(=初期個体群)は遺伝子(gene)の集まりで,ランダムに何体か生成する. |
●
| 適応度とは,淘汰の度合いを示す因子で,適応度の高い遺伝子は生き残り,そうでない遺伝子は淘汰される.適応度は GA が適用される分野に合わせて設定される.なお,適応度の計算は個体ごとに行うので,同時に(concurrently)実行してよい. |
●
| 両親の選択であるが,最も受け入れられている方法が,個体は適応度に比例した確率で親になれるという選択法で,それを実装したルーレット盤選択(roulette wheel selection)が良いとされている.これは,ルーレット盤を個体の適応度の大きさ順にその割合で分割しておき,回転したルーレット盤が停止した時に針の指している個体を第 1 の親,続けて第 2 の親を決めるという手法である. |
●
| 停止条件であるが,世代の最大数を決めておきそれに到達したら停止する,適応度の改善が見られなくなったので停止する,あらかじめ決めておいた時間をオーバーしたり資源(CPU やメモリ)を一定量消費したら停止する,などさまざまである. |
さらに,交叉,突然異変,エッジ再結合交叉について,もう少し詳しく補足すると次のようです.
■ 交叉(crossover)
たとえば,1, 2, 3, 4, 5, 6 はリレーション R1, R2, …, R6 を表すとする.この時,親個体 A=1-2-3-4-5-6,親個体 B=2-4-6-1-3-5 とした時(数字の並び順は対応するリレーションの結合順を表している),「一点交叉」により,子個体 C1=1-2-3-1-3-5,子個体 C2=2-4-6-4-5-6 が生まれる(この例では,交叉は中央で起こるとした).しかしながら,子個体の遺伝子もリレーション R1, R2, …, R6 の結合順を表しているとするならば,C1 には 1 と 3 が 2 度出現し,4,6 が出現していないので,R1, R2, …, R6 の結合プランとはなりえない.このような遺伝子を致死遺伝子という.C2 も同じである.このような場合,「適応度は 0」ということになる.
■ 突然異変(mutation)
通常の GA では,交叉と並び突然変異を利用して進化する.しかしながら,突然変異はそれだけでも最適解を探索し得る強力なオペレーションであり, GA の挙動に大きく影響を与えるため,状況によっては提案手法の有用性ないしは問題点を確認しにくくすると考えられる.したがって,そのような場合は突然変異は利用しないという選択肢がありうる.実際,GEQO では突然異変は考慮しないこととしている.
続けて,GEQO の実装で採用されたエッジ再結合交叉(edge recombination crossover, ERC)を例題と共に示しておきます.
■ エッジ再結合交叉(ERC)
エッジ再結合交叉とは,頂点ではなくエッジを見ることで,既存のパス(path, 経路)のセットに類似したパスを作成する演算子で,1989 年にホイットリー(D. Whitley)ら[10]によって導入され,
GENITOR アルゴリズムと名付けられました.ちなみに,GENITOR とは GENetic ImplemenTOR の略称です.巡回セールスマン問題(travelling salesman problem, TSP)に対して他の手法よりも優れた手法であるとされています[11].なお,TSP とは巡回セールスマンの最短ルートを見つける問題です.この際,巡回セールスマンは,本拠地から始めて,指定されたリストのすべての都市を正確に 1 回訪れ,その後本拠地に戻る必要があります.この問題の難しいところは,可能なツアーの数が非常に多いことで,n 都市に対して (n-1)!/2 となり,TSP は NP 困難な問題として知られています.
さて,ERC は子個体生成のために現在の要素の次の要素を決める際、2 つの親個体においてその要素の両側に隣接した 4 つの要素を候補とする手法です.それを例題で説明します.
【例題1】(エッジ再結合交叉,ERC)
ERC を,たとえば上述の「交叉」と同じ例を用いて説明すると次のようになる.1, 2, 3, 4, 5, 6 は
リレーション R1, R2, …, R6 を表すとする.同様に,親個体 A=1-2-3-4-5-6,親個体 B=2-4-6-1-3-5
とする.このとき,A では 6-1 とつながり,B では 5-2 とつながり巡回するとする.そこで,A と B
の隣接行列(adjacency matrix)を作ると次のようである.
A B
1: 2, 6 1: 3, 6
2: 3, 1 2: 4, 5
3: 4, 2 3: 5, 1
4: 5, 3 4: 6, 2
5: 6, 4 5: 2, 3
6: 1, 5 6: 1, 4
続いて,A と B の隣接行列の和(union)をとる(重複は除去)と次のようである.
A∪B
1: 2, 3, 6
2: 1, 3, 4, 5
3: 1, 2, 4, 5
4: 2, 3, 5, 6
5: 2, 3, 4, 6
6: 1, 4, 5
このとき,交叉による新しい個体(=遺伝子)を次のように生成する.
(1) 1~6 の数字をランダムに 1 つ選ぶ.ここでは,1 を選んだとする.
(2) 隣接集合から 1 を削除する.その結果,次の隣接行列を得る.
A∪B
2: 3, 4, 5
3: 2, 4, 5
4: 2, 3, 5, 6
5: 2, 3, 4, 6
6: 4, 5
(3) 1: 2, 3, 6 であったから,2, 3, 6 のうち,最も小さい集合を持つ 6: 4, 5 を選択する.
1-6 となる.
(4) 隣接集合から 6 を削除する.その結果,次の隣接行列を得る.
A∪B
2: 3, 4, 5
3: 2, 4, 5
4: 2, 3, 5
5: 2, 3, 4
(5) 6: 4, 5 であったが,4 も 5,どちらの隣接点の数も同じなので,ランダムにどちらかを選択
する.ここでは,4 を選んだとする.1-6-4 となる.
(6) 隣接集合から 4 を削除する.その結果,次の隣接行列を得る.
A∪B
2: 3, 5
3: 2, 5
5: 2, 3
(7) 4: 2, 3, 5 であったが,いずれも隣接点の数が 2 と同じなので,ランダムにどれかを選択する.
ここでは,3 を選んだとする.1-6-4-3 となる.
(8) 隣接集合から 3 を削除する.その結果,次の隣接行列を得る.
A∪B
2: 5
5: 2
(9) 3: 2, 5 あったが,いずれも隣接点の数が 1 と同じなので,ランダムにどれかを選択する.
ここでは,5を選んだとする.1-6-4-3-5となる.
(10)隣接集合から 5 を削除する.その結果,次の隣接行列を得る.
A∪B
2: φ
(11)したがって,1-6-4-3-5-2 が親個体 A と B のエッジ再結合交叉により作成された子個体となる.
上記のアルゴリズムから「交叉」の項の説明で見られたような致死遺伝子は子個体として発生しないことが分かる.
3. GEQO
3.1 結合質問処理の最適化と GA
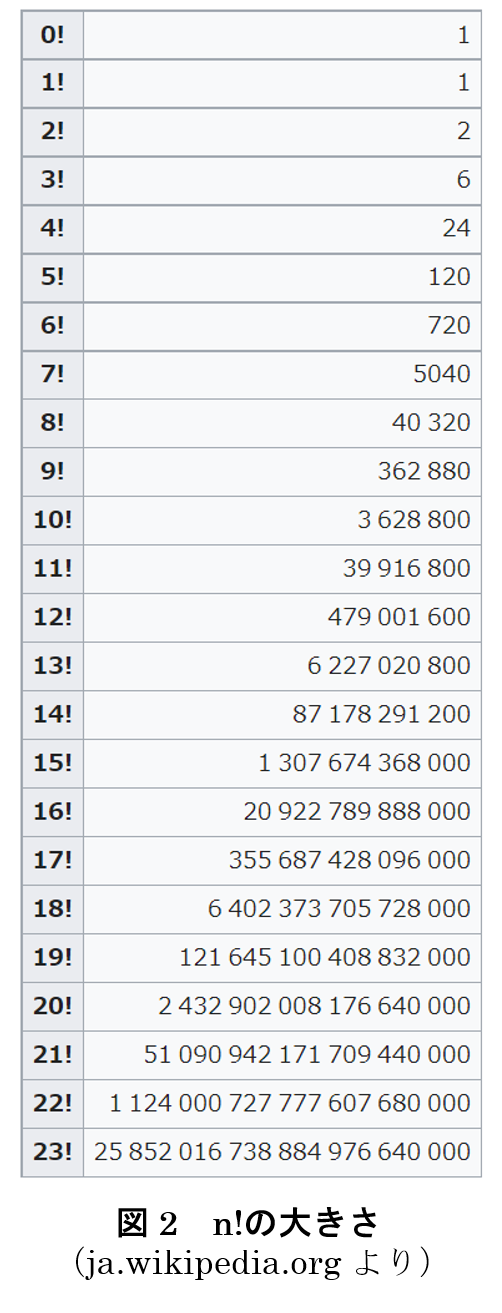
ユーティッシュが GEQO を発想した根底には,結合質問処理の最適化は,それを忠実に行えば,そのための処理に指数時間かかる扱いづらい問題であるとの認識があったと考えられます.このことは,多くのことを語らなくても,すぐに実感できます.一般に,n 個のリレーションの自然結合 R1⋈R2⋈ … ⋈Rn をとるとき,それらの結合を,たとえば (….((R1⋈R2)⋈R3)⋈…⋈ Rn-1)⋈Rn) という具合に結合を左から右へ順番にとっていくとしただけでもリレーションの並び順は n!(n の階乗)通りあります.n!が n の増加と共に,どれほど大きくなるかを図 2 に示される通りですが,見ての通り n が大きくなるにつれて n! は爆発的に大きくなります.たとえば n=10 では 360 万通りを越え,n=15 では 1 兆 3 千万通りを超えています.多数のリレーションの結合質問処理の最適プランを馬鹿正直に見つけようとすると,大変なことになるだろうとは容易に想像がつきます.
次に指摘しておきたいことは,ユーティッシュは最適なリレーションの結合順を見つける問題と巡回セールスマン問題(travelling salesman problem, TSP)とが同根であることに着眼したことです.GA は TSP のような NP 困難な「組合せ最適化問題の準最適解を与える」ために大変有効な手法であることが知られています.最適解ではなく準最適解になることは,得られる解が初期集団(=初期個体群)をどう選ぶかによるということです.上述のエッジ再結合交叉(edge recombination crossover, ERC)は TSP の準最適解を求めるのに特に適していることが知られていますが,ユーティッシュが GA を PostgreSQL に実装するにあたって ERC を採用したことは十分に理解できることです.
3.2 左深層木
結合質問処理の最適化に GA を適用しようと考えると,結合質問の処理に一つ大きな制約が課せられます.それが,リレーションの結合は左深層木(left-deep tree)で示される順番で行われなくてはならないということです.
これはどういうことかを例題で見てみます.そこで,リレーションを R1(A, B),R2(B, C, D),R3(C, E),R4(D, F),R5(E, G) とし,それらの自然結合(natural join)をとる問合せを考えてみます.

この結合質問(1)の結合グラフ(join graph)は図 3 に示される通りです.
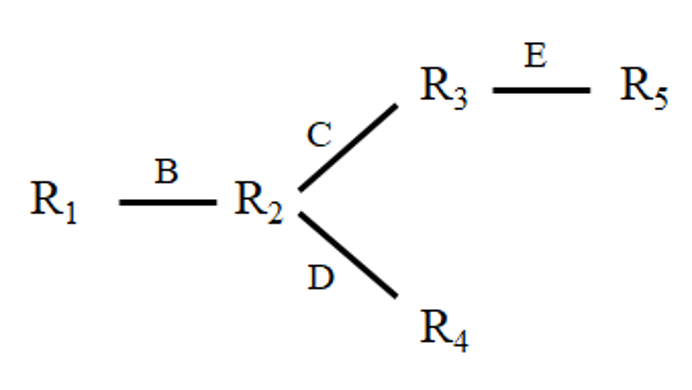
図 3 自然結合質問(1)の結合グラフ
さて,この結合質問(1)を処理するための {R1, R2, R3, R4, R5} の結合順はさまざまです.たとえば,
R1⋈((R2⋈R4)⋈(R3⋈R5)) という結合順で結合をとることもできますが,(((R1⋈R2)⋈R3)⋈R4)⋈R5 という結合順で結合をとることもできます.それらを木(tree)で表現してみると,前者は図 4(a)のように,後者は同図(b)に示されるようになります.このとき,図 4(a)のように表される木を低木(bushy tree)といい,同図 (b) のように表される木を左深層木といいます.GEQO は結合質問処理の最適化
問題をあたかもよく知られている巡回セールスマン問題(TSP)のように扱うので,候補となった
{R1, R2, R3, R4, R5} の結合順は 1’-2’-3’-4’-5’ ,つまり (((R1’⋈R2’)⋈R3’)⋈R4’)⋈R5’ と表され,これすなわち左深層木ということです(ここに,i’∈{1, 2, 3, 4, 5}∧1’≠2’≠3’≠4’≠5’).
なお,結合順は左深層木となったことにより,最適プランは本当は低木で表される結合順であった
かもしれないが,GEQO ではそれは仕方のないことということです.
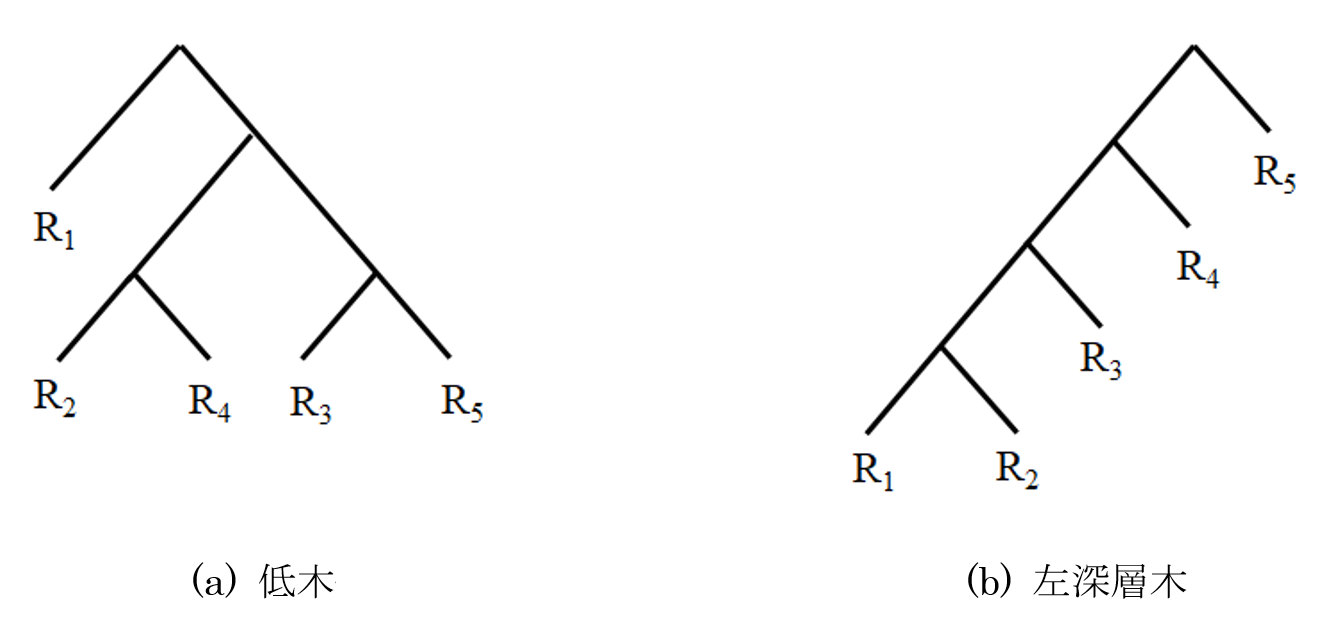
図 4 低木と左深層木
3.3 GEQO の実装
GA に基づく GEQO 実装の基本方針は次のようです.
①
| 世代全体を置換するのではなく,母集団に最も適応しない個体を置換して世代を進める.その結果,問合せプランの改善に向けた迅速な収束が可能になる.これは,妥当な時間で問合せを処理するため不可欠である. |
②
| GA による TSP 解決のためのエッジ再結合交叉 (ERC) を使用する. |
③
| 正当な TSP ツアーを生成するための修復メカニズムが必要ないように,遺伝子演算子としての突然変異は非推奨とする. |
少しばかり補うと,① は 2 章で述べた一般的な GA の適応度の概念に同じです.②は実装に「TSP 用に設計された GA アルゴリズム」として知られる GENITOR を使用しているので,交叉を「エッジ再結合交叉」を用いて行うということです.③ は「突然異変」の項で述べたことに通じる判断と考えられますが,GEQO では突然異変は考えないということです.
この基本方針の下での,GEQO の実装は,基本的に図 2 に示した GA のアルゴリズムの流れに沿ってなされていますが,より細かくは次の通りです.
(a)
| GEQO は各リレーションのスキャンをするときのコードは標準のプランナコードを使用する. |
(b)
| 結合プランは遺伝的アプローチで作成される. |
(c)
| 各結合プランは実リレーションの結合順で表現される. |
(d)
| 一番最初のステージでは,GEQO は結合順を幾つかランダムに与える. |
(e)
| 各結合シークエンスのコストを PostgreSQL の標準プランナで推定する(この時,入れ子型ループ結合法,マージ結合法,ハッシュ結合法という 3 つの結合ストラテジ全て,並びにすべての予め決められていたリレーションスキャンのプランが勘案され,その中で最安のコストが推定コストとなる). |
(f)
| 推定コストの低い方が「より適している」. |
(g)
| GEQO は「最も適していない候補」(the least fit candidates),すなわち最も適応度の低い候補,を捨てる. |
(h)
| 残った候補の遺伝子を組み合わせて新しい候補を作る.すなわち,既知の低コストの結合シーケンスからエッジ再結合交叉を使用して新しいシーケンスを検討のために作成する. |
(i)
| このプロセスを結合シークエンスが予め設定された数になるまで繰り返し,続いて,最良の結合シーケンスを見つけてそれを最終プランとする. |
3.4 GEQO のパラメタ
GEQO のパラメタは PostgreSQL 14.5 Documentation[12]に基づけば表 1 の通りです.
表 1 GEQO のパラメタ
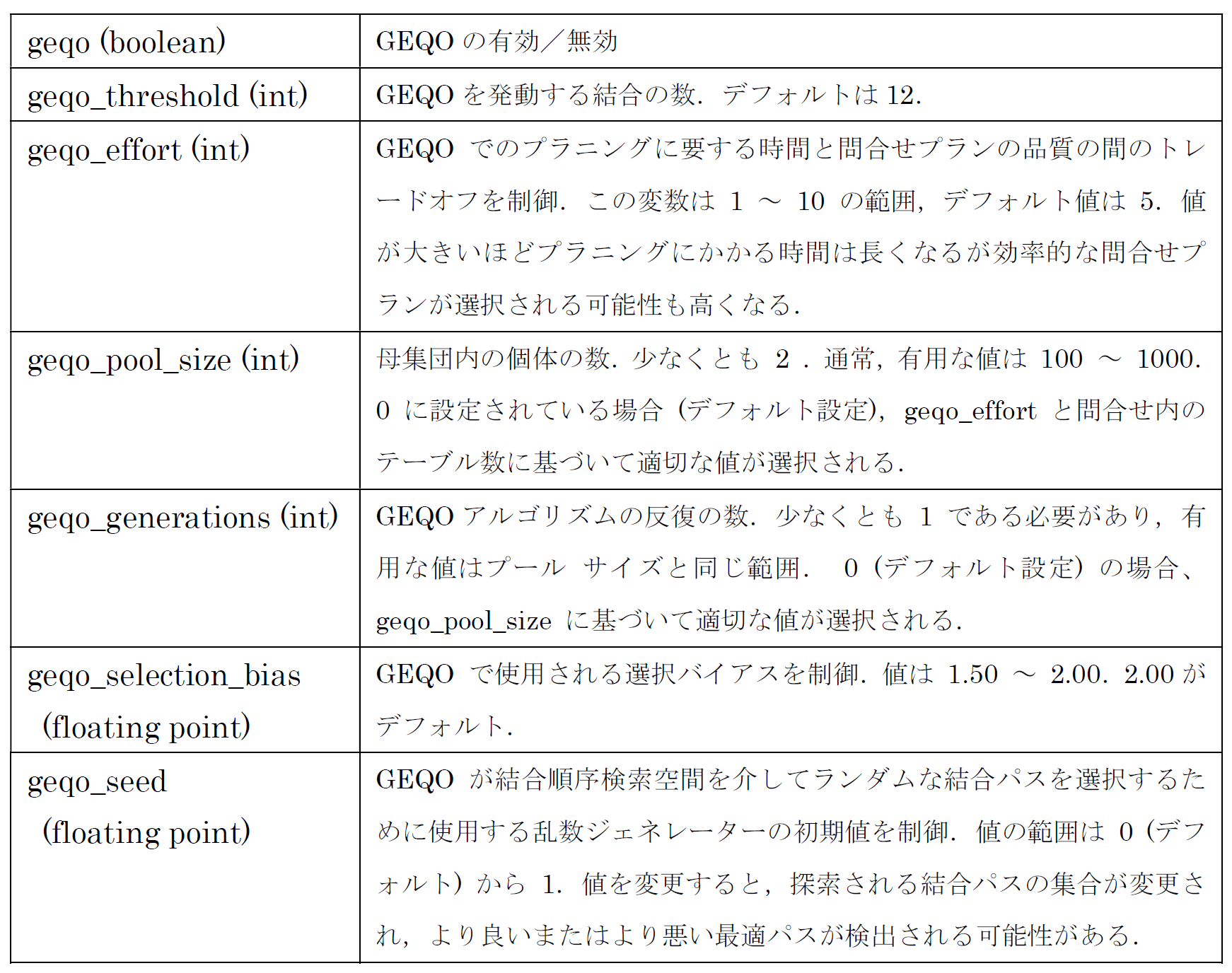
なお,PostgreSQL 14.5 Documentation に「GEQO は,ヒューリスティック検索を使用して問合せプランニングを行うアルゴリズムです.これにより,複雑な問合せ(多くのリレーションを結合する問合せ)のプラニング時間(planning time)が短縮されますが,作成されるプランは,通常の網羅的検索アルゴリズムによって検出されるプランよりも劣ることがあります」との記載があります.これは(突然異変は考えていないので)geqo_seed パラメタの値の設定によっては,GEQO を使わない通常の場合より悪いプランを出力してしまう可能性のあることを言っているのだと考えられます.
4. GEQO の評価
4.1 GEQO の評価の観点
GEQO は PostgreSQL 6.1 以降,現在に至るまでサポートされていますが,上記の qeqo パラメタを見るとき,GEQO の性能評価について,様々な観点が浮かび上がってきます.たとえば,次の通りです.
(a)
| geqo_threshold については,geqo_threshold=12 がデフォルトと設定されていますが、その妥当性の検証. |
(b)
| geqo_generations の数はどれほどに設定すればよいのか,その数の検証. |
(c)
| geqo_seed の値の設定.「さまざまな検索パスを試すには,geqo_seed を変更してみてください」とあるが,一体どれぐらい試せばよいのか?これは最初に与えるランダムな結合シークエンスを何個に指定するかということであるが,この数は結合するリレーションの数や各リレーションのアクセスパスなどにより変化するのではないか? |
(d)
| GEQO の収束条件はどのように設定されているのか? |
なお,geqo_threshold については,「FULL OUTER JOIN の生成子は,1 つの FROM 項目として計算することに注意してください」との注意書きが添えられています.これは, T1 FULL OUTER JOIN T2 を,まず T1 と T2 の内部結合を行い,その後,T2 のどの行の結合条件も満たさない T1 の各行については,T2 の列を NULL 値として結合行を追加し,さらに,T1 のどの行でも結合条件を満たさない T2 の各行に対して,T1 の列を NULL 値として結合行を追加して求めているという PostgreSQL の内部処理の事情を反映してのことでしょう.
4.2 GEQO の性能評価
かつて Petković[13]により GEQO の性能評価が報告されています.この報告は 2010 年になされており,性能評価に使用された PostgreSQL の version も 8.4 と古いので,最近の PostgreSQL の GEQO の性能を評価する参考になるのか不安になり調査したところ,次に示すように,当時の GEQO がほぼそのまま PostgreSQL 14 でも稼働しているようなので,Petković による報告には一顧の価値があると考え,それを紹介することとします.
その古き GEQO と最新の GEQO の比較調査の結果ですが,まず,PostgreSQL 8.4.22 文書(documentation)[14]にあたってみると,「49.3.2. PostgreSQL GEQO の今後の実装作業」という項目に“遺伝的アルゴリズムのパラメータ設定を改善するためにはまだ課題が残っています”として当時の実装の問題点を記載しています.一方,最新の PostgreSQL 14.5 文書[12]にあたってみると,そこにも「60.3.2. PostgreSQL GEQO の今後の実装作業」という項目があり, PostgreSQL 8.4 当時と一字一句変わらぬ文が記載されています.つまり,(プランナ本体にはこれまで幾つか改善がなされてきたのでしょうが)GEQO 自体に PostgreSQL 8.4 で指摘された改善点がこれまで施された様子は見受けられません.なお,GEQO について PostgreSQL 8.4 と PostgreSQL 14.5 で唯一記述に変更のあった部分は,
PostgreSQL 8.4 文書の「49.3.1. Generating Possible Plans with GEQO」の末尾の文 “Hence different plans may be selected from one run to the next, resulting in varying run time and varying output row order.” が,PostgreSQL 14.5 文書の「60.3.1. Generating Possible Plans with GEQO」では,“To avoid surprising changes of the selected plan, each run of the GEQO algorithm restarts its random number generator with the current geqo_seed parameter setting. As long as geqo_seed and the other GEQO parameters are kept fixed, the same plan will be generated for a given query (and other planner inputs such as statistics). To experiment with different search paths, try changing geqo_seed.” と変更になっているだけです.ただ,これは上記 4.1 節の(c)項に関する記述変更で,
GEQO 本体レベルの変更ではないと推察され,GEQO の実装は現在も当時のままのようです.
さて,その報告では,2 つの実験結果が示されており,それらは 4.1 節の(a)項と(b)項に対応して
いるようです.一つは,geqo パラメタで,GEQO を有効としたときと無効としたときの結合質問の
実行時間の比較です.PostgreSQL 8.4 では実行時間は total run time を意味するので,プランナが
消費した時間と最適プランをエグゼキュータがその実行に消費した時間を個別に評価することは
できず,2 つを足し合わせた時間です.もう一つは,GEQO を有効としたとき,GEQO アルゴリズムの反復数(geqo_generations),つまり世代数の変化が結合質問の処理時間に与える効果です.これは,世代数を大きくすれば,結合プランの質が高まり,その結果,結合質問の処理速度が向上するだろうことを期待した検証といえます.
まず,実験を行うには,結合数が 10 を超えるような結合質問を多数用意する必要がありますが,
PostgreSQL 8.4 の元々のサンプルデータは 6 枚のテーブルしか持っていないので,大きな結合を試せず,MS SQL Server システムのサンプルデータである Adventure Works 2008 を PostgreSQL にインポートして使用したと報告しています.そこには 60 枚以上のテーブルがあるとのことで,そのうちの幾つかを表 2 に示します.評価にどのようなテーブルが使われたのか,それをイメージしていただければよいかと思います.
表 2 実験に使われたテーブル(の一部)

テストのための問合せは表 3 に示される “generic query”(一般的問合せ)を考え,それから他の問合せを導出し,最大 14 個の結合演算を含む 18 個の問合せを作成して走らせたと報告しています.
表 3 実験に使われた結合質問(一般的問合せ)

この内結合質問は 13 個のテーブルを使い,そこでは 12 個の結合演算が定義されています.ちなみに,この問合せの「結合グラフ」を作成してみると図 5 のように描けます.
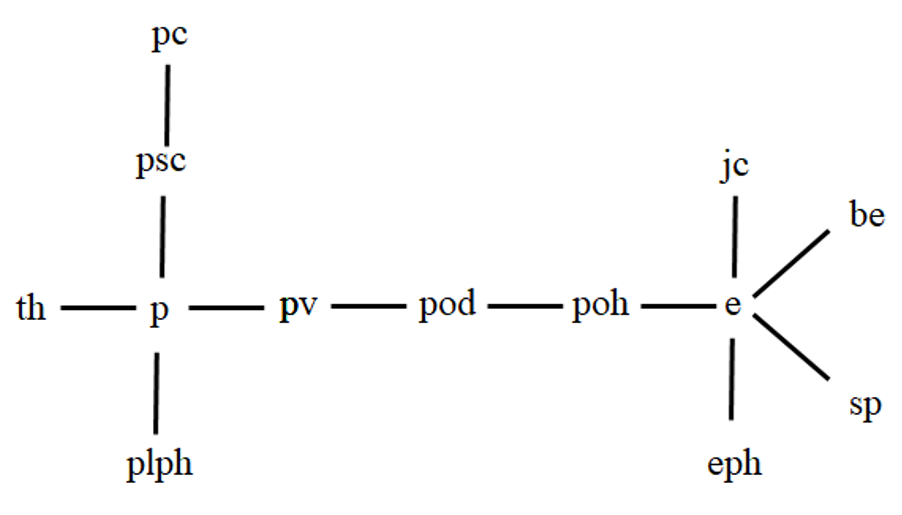
図 5 実験に使われた結合質問の結合グラフ
GEQO はこの結合グラフを基に,左深層木で表される線形順序の結合プランを幾つかランダムに生成して初期集団を作成し,GENITOR に入力しているということになります.幾つもの左深層木が定義できます.興味を抱いた読者は試してみてください.
続いて,実験結果を紹介します.
【実験結果1】GEQO モジュール vs. 全数探索
PostgreSQL が GEQO を無効にして,つまり全数探索(exhausted search)にて結合質問処理の最適化を行った場合の問合せの実行時間と GEQO モジュールを有効にして結合質問処理の最適化を行った場合の問合せの実行時間の比較を行います.なお,全数探索(exhausted search)という用語を PostgreSQL 14.5 文書[12]も Petković[13]も用いていますが,プランナは n 個のテーブルの結合の
コスト最小プランを見つけるために n! 個の結合順すべてにあたっているわけではなく,コストベー
スアプローチ(=DP アプローチ)でそれを行っているので,全数検索というよりはコストベース
アプローチと表現するほうが適切でしょう.
さて,比較の対象とした問合せは,11,12,13,14 個のテーブル結合を有します.図 6 はそれら
の問合せ全てに対する平均実行時間を結合するべきテーブルの数でまとめています.各結合数に対し
て,左側の縦棒は GEQO が有効,右側が無効のときを表します.図から分かるように,両者は結合
演算の数が 12 までは互角です.しかしながら,12 を超えると,GEQO はコストベースアプローチ
(=GEQO が無効)に比べて約 15% 越えの効果を発揮しています.実験では,14 を超える場合を
検証していませんが,同様な効果が期待できると報告しています.つまり,テーブルの結合数が 13
以上の場合,GEQO を有効にすると,無効にしていた時と比べて少なくとも 15% 速く結合質問が
処理されるであろう,ということです.PostgreSQL 14.5 文書は geqo_threshold=12 で GEQO に
切り替わるとしていますが,geqo_threshold=13 でよいということになります.なお,この実験で
は,世代数 geqo_generation を幾つに設定したのか記載がありませんが,もしデフォルトで実験を
行ったとすれば geqo_generation=0 なので,その場合,表 1 に記されたように,geqo_pool_size
に基づいて適切な値が選択されているということになります.
![GEQO モジュールとコストベースアプローチの比較[13]](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/11/drmasunaga-10-P15-01a.png)
図 6 GEQO モジュールとコストベースアプローチの比較[13]
【実験結果2】世代数を増していった時の効果
GEQO を有効とした場合,結合質問の実行時間を GEQO アルゴリズムの反復数(geqo_generations),つまり世代数をパラメタに比較しています.geqo_generation パラメタを 1,すなわち世代数を 1 から始めて,13 まで検証した結果が図 7 です.図が示しているように,世代数を大きくするにつれて,オプティマイザはより最適な実行プランを求めることができて,結合質問の実行時間は減少していくことを示しています.geqo_generation=1 では問合せ 1 個当たりの平均実行は最適の場合に比べて約 25% 余計にかかっていることが示されています.世代数を 9 世代,すなわちgeqo_generation=9 で最適値に収束するようです.したがって,そのように設定しておくとよいのかもしれません.
![世代数の変更の効果[13]](https://www.sraoss.co.jp/tech-blog/wp-content/uploads/2022/11/drmasunaga-10-P16-01a.png)
図 7 世代数の変更の効果[13]
5.おわりに
PostgreSQL の結合質問処理の最適化モジュールである GEQO を概観しました.PostgreSQL 14.5 では geqo_threshold パラメタで GEQO を発動するリレーションの結合の数のデフォルトは 12 と定めていますが,紹介した実験結果によればその数は 13 のようです.あまり大した差ではありませんが,そこら辺が目安ということなのでしょう.
改めて言うまでもありませんが,リレーショナルデータベースの最大の特徴はデータベース言語 SQL が非手続き的(non-procedural)であるところにあり,それが故に質問処理の最適化は永遠の課題でもあります.質問処理最適化の研究・開発は機械学習の適用で一段と深まりを見せ,佳境に入った感があります.今後の理論展開と実践に注目し続けたいと思います.
【文献】
[1]
| Patricia Selinger, M. Astrahan, D. Chamberlin, Raymond Lorie, and T. Price. “Access Path Selection in a Relational Database Management System.” Proceedings of ACM SIGMOD (1979), pp. 23-34, 1979. |
[2]
| Martin Utesch. Chapter 60. Genetic Query Optimizer, PostgreSQL 14 Documentation, The PostgreSQL Global Development Group, 2022. |
[3]
| Tomas Kovarik and Julius Stroffek. Execution plan optimization techniques. PGcon 2007. |
[4]
|
Jan Urbański. Replacing GEQO – Join ordering via Simulated Annealing. PGCon 2010. https://www.pgcon.org/2010/schedule/events/211.en.html |
[5]
|
Oleg Ivanov. Adaptive query optimization in PostgreSQL. PGCon 2017. https://www.pgcon.org/2017/schedule/events/1086.en.html |
[6]
| Miguel Rodríguez, Daladier Jabba, Elias Niño, Carlos Ardila and Yi-Cheng Tu. Automata Theory based Approach to the Join Ordering Problem in Relational Database Systems. Proceedings of the 2nd International Conference on Data Technologies and Applications (DATA-2013), pp.257-265, 2013. |
[7]
| Ryan Marcus, Parimarjan Negi, Hongzi Mao, Chi Zhang, Mohammad Alizadeh, Tim Kraska, Olga Papaemmanouil, Nesime Tatbul. Neo: A Learned Query Optimizer, Proceedings of the VLDB Endowment, pp.1705-1718, 2019. |
[8]
| John Henry Holland. Adaptation in Natural and Artificial Systems (book). MIT Press, 1975. |
[9]
| Eyal Wirsansky. Hands-On Genetic Algorithms with Python: Applying genetic algorithms to solve real-world deep learning and artificial intelligence problems, Packt Publishing, 2020. |
[10]
| Darrell Whitley. The GENITOR Algorithm and Selection Pressure: Why Rank-Based Allocation of Reproductive Trials is Best. Proceedings of the Third International Conference on Genetic Algorithms (ICGA-89), pp. 116-121, Morgan Kaufmann Publishers Inc., San Francisco, 1989. |
[11]
|
Wikipedia (en). Edge recombination crossover. https://en.wikipedia.org/wiki/Edge_recombination_operator |
[12]
|
The PostgreSQL Global Development Group. PostgreSQL 14.5 Documentation. https://www.postgresql.org/files/documentation/pdf/14/postgresql-14-A4.pdf |
[13]
| Dušan Petković. Comparison of Different Solutions for Solving the Optimization Problem of Large Join Queries. Proceedings of the 2010 Second International Conference on Advances in Databases, Knowledge, and Data Applications, pp.51-55, 2010. |
[14]
|
PostgreSQL 8.4.22 Documentation. Chapter 49. Genetic Query Optimizer. 49.3. Genetic Query Optimization (GEQO) in PostgreSQL. 49.3.2. Future Implementation Tasks for PostgreSQL GEQO. https://www.postgresql.org/docs/8.4/geqo-pg-intro.html#GEQO-FUTURE |