増永教授のDB特論⑫「ビューサポートの基礎理論」

1. はじめに

 ビュー（view）はリレーショナルデータベースの始祖コッド（E.F. Codd）がリレーショナルデータモデル[1]を世に問うてから 4 年後の 1974 年に彼自身により導入されました[2]．ビューは定義だけが存在し実体は伴わない仮想的なリレーションであるところがデータベースに格納されているリレーション，これを実リレーション（stored relation）という，と根本的に異なるところです．

 ビューは質問変形（query modification）と呼ばれる手法[3]により，ビューに対するいかなる「質問」（query，問合せ）も常に実行可能です．これは理論でも実践（=SQL）でもその通りです．つまり，ビューへの問合せは常にサポートされているということです．しかしながら，ビューを「更新」（update）しようとすると一筋縄ではいかなくなります．つまり，更新できるビューもあれば更新できないビューもあります．その理由は「ビューは実リレーションではなくあくまでも仮想的なリレーションであるから」です．では，一体どのような条件を満たすときに，ビューは更新可能となるのでしょうか？これはビュー更新問題（view update problem）と呼ばれ，コッドがビューを提案した当初からさまざまな研究がなされて現在に至っています．
さて，ビュー更新問題は理論的にはビュー定義の逆関数を一意に不都合なく決定できるか否かという問題として定式化できますが，一意性には意味論（semantics）が関わってくること，逆関数の存在をタップルの重複出現を許さない集合意味論のもとで論じるのか，そうではなく（SQL テーブルのように）タップルの重複出現を許すバッグ意味論のもとで論じるのかという立場の違い，あるいは逆関数の存在を従来のようにリレーションスキーマレベルで問うのか，そうではなくインスタンスレベルで問うのか，などさまざまな観点があり，それによりビューの更新可能性に大きな変化が生じることともなり，今なお，ビュー更新問題は解決済みとは言い難い状況です．
このような認識のもと，本稿では「ビューサポートの基礎理論」と題して，ビューとその更新可能性の概念，ビューの更新可能性をスキーマレベルで論じることとインスタンスレベルで論じることとの違い，スキーマレベルにおけるリレーショナルビューとバッグビューの更新可能性の違いなど，ビューサポートに関するさまざまな観点を念頭に置きつつ諸概念を整理しながら議論することで，そこから見えてくるビューサポートの全貌を報告してみたいと思います．

2. ビューとその更新可能性

2.1 ビューとは

 ビューとその更新可能性をリレーショナルデータモデルの観点から論じるとき，その基礎となるのはリレーショナル代数（relational algebra）です．一方，SQL のテーブルを念頭においてビューとその更新可能性を考えると，SQL ではタップルの重複出現を許すテーブル，これをバッグ（bag）という，の存在を前提としているので，その基礎となるのはバッグ代数（bag algebra）です．そこで，本稿ではリレーショナル代数で定義されるビューをリレーショナルビュー，バッグ代数で定義されるビューをバッグビューと呼び両者を区別します．

 さて，リレーション R(A₁, A₂, _…, A_n) は dom(R)=dom(A₁)✕dom(A₂)✕・・・✕dom(A_n) の有限部分集合として定義されます．ここに dom(A_i) は属性 A_i がとりうる値の全集合を表します．では，ビューは一体どのように定義されるのでしょうか？その詳細な定義は 3.1 節で与えますが，たとえば，リレーション R(A₁, A₂, _…, A_n) の選択ビューV は V=σ_φ(R(A₁, A₂, _…, A_n)) と定義されます．ここに，φ は dom(R) の元を引数とする述語で，σ_φ はリレーショナル代数演算で選択（selection）を表します．バッグビューの定義は 4.1 節で与えますが，たとえば R(A, B) と S(A, B) を和両立なバッグとした時，
R と S の加法和ビュー V は V(A, B)＝S(A, B)⨄R(A, B) と定義されるということです．ここに，⨄ は
加法和を表すバッグ代数演算で，これはリレーショナル代数にはないバッグ代数に特有の演算です．

 理論上，リレーショナルビューはバッグビューの特殊な場合となるのですが，まずリレーショナルビューの更新可能性を論じ，それが拡張される形でバッグビューの更新可能性を論じる方がビューサポート理論の全貌を見通しやすいと考えられるのでそのような展開とします．本章では引き続きビューとその更新可能性について論じ，続く第 3 章でリレーショナルビューの更新可能性を，第 4 章でバッグビューの更新可能性を論じます．

2.2 ビューの更新とは

 ビューの更新（update）とは，ビューは仮想的な構成体（construct）であるにも関わらず， SQL の用語を借りればビュー表（viewed table）として，あたかも実リレーションや実バッグであるかのように捉えてビューを更新しようとすることをいいます．しかしながら，ビューには実体がないことから更新できる場合もあればできない場合もあります．

 更新には，削除（delete），挿入（insert），書換（rewrite）があります．まず，削除と挿入を定義します．ここに dom(V) はビュー V のドメインを表します．

   削除（d）：delete σ_φ(V) from V; ここに φ は dom(V) の元を引数とする述語である．
挿入（i）：insert X into V; ここに X⊆dom(V) とする．

 リレーショナルビューの削除と挿入の定義は次の通りです（バッグビューの削除と挿入の定義は 4.2 節で与えます）．

● 削除（d）は，リレーショナル代数表現で表せば d: V←V－σ_φ(V) と定義するということです．
ここに－は差，φ は V に対する選択条件で，←はリレーションの置換を表します．
● 挿入（i）は，リレーショナル代数表現で表せば i: V←V∪Xと定義するということです．
ここに∪は和を表します．

ここで，ビューのドメインと書換について補足説明を行います．

■ ビューのドメインについて

 ビュー V(A_1’, A_2’, _…, A_r’) のドメイン dom(V) は，一般に dom(A_1’)×dom(A_2’)×・・・×dom(A_r’) そのものではなく，ビュー定義を満たすその部分集合として定義されます．

 たとえば，リレーション R(A, B) の選択ビューを V(A, B)=σ_B≦b(R(A, B)) とした場合，
dom(V)=dom(A)×dom(B) ではなく， dom(V)=dom(A)×σ_B≦b(dom(B))となります．具体的には，リレーション社員(社員番号，給与)を実リレーションとし，ビューを貧乏社員=σ_給与≦20(社員) とした時，dom(貧乏社員)= dom(社員番号)×σ_給与≦20 (dom(給与)) と定義されます．その結果，ビュー貧乏社員に対して，挿入 insert {(100, 10), (101, 15)} into 貧乏社員; は受け付けられてその更新可能性が検証の対象となりますが，insert {(100, 10), (101, 40)} into 貧乏社員; は (101, 40) の存在により {(100, 10), (101, 40)}⊆dom(貧乏社員) とはならないのでビュー貧乏社員に対して発行できる挿入ではないということです．つまり，上記の dom(V) の定義はビューの持つ意味に抵触するような挿入をあらかじめ排除する意図があります．これにより，リレーショナル DBMS は発行された挿入がビュー定義に抵触しないか否かの検証，これはインスタンスレベルの検証となります，を行わなくて済むので大いに助かりますが，一方でクライアントにはビューの定義に抵触しない挿入を発行しなければならないことが求められます．この条件はビュー更新を（本稿では）スキーマレベルで論じたいから課せられた条件ということです．
dom(V) の他の基本的な例としては，V＝R ならば dom(V)=dom(R) です．R と S を和両立とするとき和ビュー V=R∪S や差ビュー V=R－S のドメインは dom(V)=dom(R)=dom(S) です．直積ビュー V=R×S のドメインは dom(V)=dom(R)×dom(S) です．リレーション R(A₁, A₂, _…, A_n) の属性集合 X（⊆Ω_R），ここに Ω_R ={A₁, A₂, _…, A_n}，上の射影ビュー V=π_X(R) のドメインは，X={A_1’, A_2’, _…, A_r’}，ここに 1≦1’≦2’≦…≦r’≦n として，dom(V)=dom(A_1’)×dom(A_2’)×･･･×dom(A_r’) となります．選択ビューについては上記の通りです．R(A, B) と S(B,C) の等結合ビュー V(A, R.B, S.B, C)=
R⨝_R.B=S.BS のドメインは dom(V)=σ_R.B=S.B(dom(A)×dom(R.B)×dom(S.B)×dom(C)) となります．
R(A, B) と S(B,C) の自然結合ビュー V(A, R.B, C)=R⨝S のドメインは dom(V)=π_{{A, R.B, C}}(σ_R.B=S.B
(dom(A)×dom(R.B)×dom(S.B)×dom(C))) となります．リレーショナル代数演算を複合して適用して定義される一般的ビュー，たとえば，リレーション R(A, B, C)の選択と射影で定義されるビュー V=π_{{A, B}}(σ_C=c(R)) のドメインは dom(V)=dom(A)×dom(B) です．これは，中間ビュー V₁=σ_C=c(R) のドメインは dom(V₁)= dom(A)×dom(B)×σ_C=c(dom(C))ですが，V のドメインは dom(V₁) の {A, B} 上の射影をとって定義されているのでそうなります．このようにビューのドメインはいずれもビュー定義と表裏一体の関係で定義されます．

■ 書換について

本稿では書換を削除と挿入の系列とみなします．このとき，ビューの削除は可能であったとしても，続く挿入には注意を払う必要があります．どういうことかを上記のビュー貧乏社員=σ_給与≦20(社員)を例にすれば次の通りです．たとえば，社員番号 200 の社員の給与が 15 であったとすると，タップル (200, 15) がビュー貧乏社員に出現します．給与倍増ということで，社員番号=200 の給与を 30 に書換えるとします．このとき，書換は削除と挿入の系列とみなしているので，まずビュー貧乏社員から (200, 15) を削除して，続いて (200, 30) が挿入されるということです．3.2 節[11]項で示される通り，選択ビューは削除可能なのでビュー貧乏社員からの (200, 15) の削除は基底リレーション社員からの (200, 15) の削除に変換できます．しかしながら，続く，ビュー貧乏社員への (200, 30) の挿入は挿入の条件である {(200, 30)}⊆dom(貧乏社員)，ここに dom(貧乏社員)=dom(社員番号)×σ_給与≦20 (dom(給与))，とはならないので許されません．これは社員番号が 200 の社員は給与が 30 なのでもはや貧乏社員ではないので当然のことです．つまり，給与が倍増されたこの社員はビュー貧乏社員に挿入されるべきではなく，基底リレーション社員に直接挿入されるべきなわけです．つまり，(200, 30) をビュー貧乏社員に挿入するすべがないのではなく，それはリレーション社員に挿入され，その結果として社員番号 200 の社員はビュー貧乏社員には現れなくなる，それがビューの更新を考察する場合の「書換は削除と挿入の系列とみなす」の意味と処理です．

2.3 ビューの更新可能性

 一般にビューは仮想的な構成体なので，実リレーションや実バッグと異なりすべてのビューが更新可能とは限りません．ビューはどのようなときに更新可能となるのか，それをダヤール（U. Dayal）ら [4] が与えた定義を参考にして規定すると次のようになります． ここにデータベーススキーマを S，時刻 τ におけるデータベース状態を S_τ（つまり，S_τ は時刻 τ における S のインスタンス），ビュー定義を V で表すと，時刻 τ におけるビュー（状態）は V_τ（=V(S_τ)）です．

【定義１】（ビューの更新可能性）
時刻 τ におけるビュー V_τ への更新 u が変換可能（translatable）であるとは，u の V_τ から S_τ への変換（translation）T が存在して，次の条件を満たすときをいう．

 (a)

変換 T は一意（unique）である．

 (b)

V_τ に副作用がない（no side effect）．

 (c)

T(u) には S_τ に対する余計な更新がない（no extraneous update）．

 (d)

T(u) はデータベーススキーマ S の一貫性制約に抵触しない．

以下，定義 1 を補足します．

 (a)

一意性

 更新可能性の大前提である変換に「一意性」を課したことは，変換 T に代替案があった時にその選択基準を設けられないためです．たとえば，リレーション R(A, B)={(1, 2)} と S(B, C)={(2, 3)} の自然結合ビュー V=R⨝S が定義されていて，V に対して削除 d=delete {(1, 2, 3)} from V; が発行されたとします．このとき，この削除を実現できる d の変換は次に示す 3 つ考えられます．
T₁(d)= delete {(1, 2)} from R;
T₂(d)= delete {(2, 3)} from S;
T₃(d)= begin; delete {(1, 2)} from R; delete {(2, 3)} from S; end;
注意するべきは，T₁(d)～T₃(d) の持つ削除の意味がそれぞれ異なるということです．意味が異なるということは勝手な選択はデータベースの一貫性に問題を生じさせかねないということです．サイコロを振ってどれかにするというようなことは許されないということです．「一意性」はデータベースの一貫性維持のために必要な制約です．

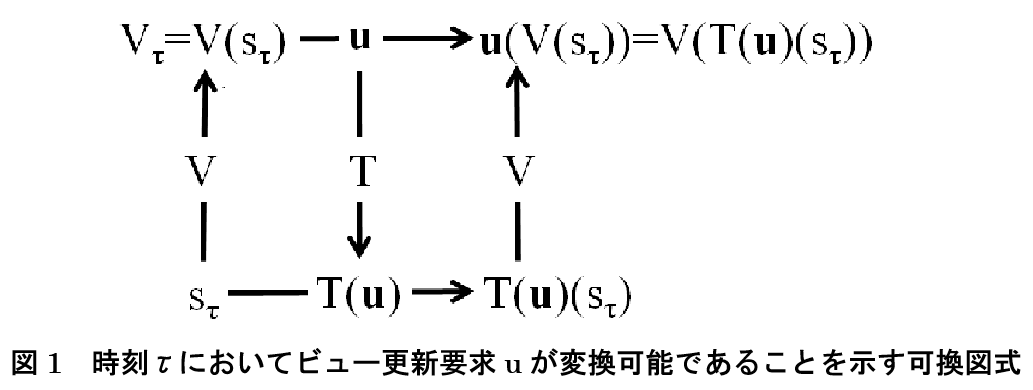
 (b)

副作用がない

 「副作用がない」とは図 1 に示す可換図式が成立することをいいます．副作用が生じる例としては，2 つのリレーションを R(A, B)={(1, 1)}, S(C, D)={(1, 1)} として，V=R×S={(1, 1, 1, 1)} を直積ビューとします．このとき，V に対して挿入 i=insert {(2, 2, 2, 2)} into V; が発行されたとします．i を R と S への挿入の系列 T(i)=begin; insert {(2, 2)} into R; insert {(2, 2,)} into S; end; に変換すれば，確かに (2, 2, 2, 2) が V に挿入されますが，同時に (1, 1, 2, 2) と (2, 2, 1, 1) が V に出現してしまいます．これを副作用といい，それは意図した更新ではなかったので，その発生の源となった挿入 i を上記のように変換することは許されないということです．

 (c)

余計な変換がない

 S_τに対する「余計な変換がない」とは，たとえば，リレーション社員(社員番号, 社員名, 給与, 部門)={(001, 山田太郎，50，K55)，(002，鈴木花子，40，K41)，(003，田中桃子，60，K41)，(004，佐藤一郎，40，K55)}，ここに社員番号は社員の主キーとする，の射影ビュー V=π_{{社員番号，社員名}}社員={ (001, 山田太郎)，(002，鈴木花子)，(003，田中桃子)，(004，佐藤一郎)} に挿入 i=insert {(007，ボンド)} into V; が発行されたとき，i をリレーション社員に対する挿入 T(i)= insert {(007，ボンド，null，
null)} into 社員; ここに null は属性に値がないことを表す，に変換すれば問題は生じませんが，そうではなく，たとえば，T’(i)= insert {(007，ボンド，100，null)} into 社員;とすると，これで確かに射影ビュー V に (007，ボンド) が挿入されますが，基底リレーション社員にはボンドの給与が 100 であるという余計な値が挿入されることになり，これは許さないということです．

 (d)

データベーススキーマの一貫性制約に抵触しない

 「データベーススキーマの一貫性制約に抵触しない」ですが，その意味するところは次の通りです．時刻 τ でビュー V に対して発行された更新 u に対して，条件 (a)～(c) を満たす更新変換 T(u) が存在したとします．このとき，時刻 τ におけるデータベース状態を S_τ で表すと，S_τ は T(u) で更新されないといけないわけですが，この更新がデータベーススキーマ S に課せられている一貫性制約に抵触してはならないということです．
一貫性制約は多様です．キー制約はすべてのリレーションに課せられている一貫性制約ですが，データベース化の対象となった実世界に存在する意味的制約を反映した一貫性制約もあります．たとえば，リレーションスキーマ社員(社員番号, 社員名, 給与, 部門)について，「各部門には最低 2 名の社員が所属していなければならない」という一貫性制約が課せられていたとします．そして，ビュー「K55 社員」を K55 社員=σ_部門=K55(社員)と定義したとします．このとき，ビュー K55 社員に対して一名の K55 社員を削除する操作が発行されたとします．ビュー K55 社員は選択ビューなので，それに対して発行された削除はそのまま基底リレーションであるリレーション社員の削除に変換可能です（3.2 項【11】項）．しかしながら，もし K55 社員が 2 名しかいなかった場合，この削除は「各部門には最低 2 名の社員が所属していなければならない」というリレーションスキーマ社員の一貫性制約に抵触するので受け付けてはなりません．これが条件 (d) の意味するところです．
しかしながら，条件 (d) はビューに特有の条件ではないことに注意する必要があります．たとえば，上記のリレーションスキーマ社員に上記と同じ一貫性制約が課せられていれば，この制約は社員のいかなるインスタンスとしてのリレーション社員に（ビューを通してではなく）直接更新がかけられたときにもそれに抵触してはならない制約です．したがって，条件 (d) を特段にビューの更新可能性の条件として課するべきではないと捉え，本稿ではビューへの更新は定義 1 の条件 (a)～(c) を満たすとき，変換可能とすることにします（関連した議論を 3.1.2 項でも行っています）．
なお，ビュー V_τ への更新 u が変換可能（translatable）であるとき，ビュー V_τ は更新可能（updatable）であるともいいます．

2.4　スキーマレベル vs. インスタンスレベルアプローチ

 リレーショナルデータモデルにはリレーションスキーマとそのインスタンスという概念区分があります．時間的に不変なリレーションの構造がリレーションスキーマ（relation schema）で，一般に時間と共に変化するコンテンツとしてのリレーションがリレーションスキーマのインスタンス（instance）です．そして，両者の関係性は次の通りです[10]．
「リレーションスキーマ R である性質 P が成り立つということは，R のすべての
インスタンス R に対してその性質 P が成り立つとき，およびそのときのみである」

 たとえば，リレーションスキーマ社員(社員番号, 社員名, 給与, 部門)があったとき「社員番号が社員のキーである」という性質は，リレーションスキーマ社員のすべてのインスタンス社員に対して次が成立することです．ここに t[社員番号]はタップル t の属性である社員番号がとる値を表します（⇒は含意を表す）．
(∀t, t’∈社員)(t[社員番号]=t’[社員番号]⇒t=t’)

さて，先に与えた定義 1 はビューの更新可能性をインスタンスレベルで規定しています．しかしながら上記の観点から定義 1 で与えられたビューの更新可能性の定義を見直すと，ビューの更新可能性を定義通りにインスタンスレベルで規定することは勿論できますが，スキーマレベルで規定することも可能であることが分かります．どちらのアプローチをとるべきなのでしょうか，素朴な疑問に直面してしまいます．
しかしながら，これまで行われてきたビューの更新可能性の議論に目を向けてみると，この問題は理論的にも実践的にもスキーマレベルで議論されてきました．なぜでしょうか？その理由は，スキーマレベルで規定することにより，与えられたビューの更新可能性をリレーショナル DBMS が検証するにあたり，検証をテーブル参照（table lookup）で行えるからです．つまり，ビューの更新可能性をスキーマレベルで規定しておくと，基本的ビューの更新可能性を予あらかじめメタデータとしてカタログに登録しておけば，一般的ビューが与えられた時，それが更新可能かどうかは，そのビュー定義を構文解析して，その構文解析木のノードに一つでも更新不可能とされる基本的ビュー定義があれば，その時点でその一般的ビューは更新不可能と判定できるからです．たとえば，「直積ビューは削除不可能」とカタログに登録されていれば，一般的ビューの定義に直積が用いられていることを見つけた時点で，このビューは削除不可能と判定できるわけです．これはビュー更新をサポートしようとするリレーショナル DBMS にとっては負荷が少なくとても嬉しく映るはずです．実際，現在のプロプライエタリあるいは OSS のリレーショナル DBMS のすべてはこのアプローチに基づいています．
一方，もしビューの更新可能性をインスタンスレベルで判定すると状況は一変します．何が変わるのかといえば，スキーマレベルで更新不可能とされるビューがインスタンスレベルでは状況により更新可能となるということです．たとえば，リレーション R(A, B) と S(B, C) の自然結合ビュー定義 V=R⨝S の更新可能性は，スキーマレベルのアプローチでは「押し並なべて結合ビューは更新不可能だから V は更新不可能」となってしまいますが，インスタンスレベルのアプローチではそうはならず，「この・・自然結合ビュー V に対して発行されたこの・・更新 u は変換可能か否か」をケースバイケースで検証していくということです．したがって，インスタンスレベルのアプローチを採るとリレーショナル DBMS の負荷は増大するのですがクライアントにとっては更新できるビューが却下されてしまうことが少なくなるので福音となります．つまり，ビューの更新可能性をスキーマレベルで規定するのかインスタンスレベルで規定するのかは処理コストと更新可能性のトレードオフということになります．筆者らが考案した「更新意図の外形的推測に基づいたビューの更新可能性」[6, 7] はインスタンスレベルの考え方に基づいたビュー更新の新しいアプローチです．興味を抱いた方は是非，拙著論文にあたってみてください．

3. リレーショナルビューの更新可能性（スキーマレベル）

3.1 リレーショナルビューの定義

3.1.1 リレーショナル代数

 リレーショナルビューはリレーショナル代数を使って定義されます．リレーショナル代数はコッドがリレーショナルデータモデルの一環として導入しましたが，以下に示す演算からなります [1]．
【定義２】（リレーショナル代数演算）
● 和（∪），差（－），共通（∩）
● 直積（×）
● 射影（π_X(R)，ここに X⊆Ω_R）
● 選択（σ_φ (R)，ここに φ は dom(R)上の選択条件）
● θ-結合（R⨝_AiθBjS，ここに A_i∈Ω_R，B_j∈Ω_S で A_i と B_j は θ-比較可能）
● 商（÷）

 これら 8 つの演算の定義を表 1 に示します．

補足をすれば次の通りです．

 ●

リレーション R の全属性集合を Ω_R={A₁, A₂, _…, A_n}としたとき，R はdom(R)=dom(A₁)×dom(A₂)×・・・×dom(A_n) の有限部分集合と定義されます．

 ●

述語 R(t) はタップル t がリレーション R の元であるとき，つまり t∈R のとき及びそのときのみ真（true）となります．

 ●

∨，∧，¬，⇒，⇔ はそれぞれ論理和，論理積，論理否定，含意，必要かつ十分，を表す命題結合子です．

 ●

タップルを結合する演算子* は (a₁, a₂, _…, a_n)*( b₁, b₂, _…, b_m)=(a₁, a₂, _…, a_n, b₁, b₂, _…, b_m) と定義されます．

 ●

R(A₁, A₂, _…, A_n) と S(B₁, B₂, _…, B_m) をリレーションとするとき，それらが和両立（union compatible）であるとは n=m∧∀_i(dom(A_i)=dom(B_i)) が成立しているときをいいます．

 ●

t =(a₁, a₂, _…, a_n) をリレーション R(A₁, A₂, _…, A_n) のタップル，Ω_R の部分集合を X={ A_1’, A_2’, _…, A_ℓ’}，1≦1’≦2’≦・・・≦ℓ’≦n としたとき，t の X 上の射影は t[X]=(a_1’, a_2’, _…, a_ℓ’) と定義されます．

 ●

比較演算子を θ∈{＜, ≦，≠，＝,＞，≧} とします．

 ●

A_i∈Ω_R，B_j∈Ω_S で A_i と B_j が θ-比較可能とは A_iθB_j の真，偽が常に決まることをいいます（3 値論理の場合は，真，偽，不定となります）．

 ●

選択を定義する際に使用される選択条件 φ は次のように再帰的に定義されます．ここに A_i や A_j はリレーション R(A₁, A₂, _…, A_n) の属性で，A_i と A_j は θ-比較可能，c を定数，θ を比較演算子とします．

【定義３】（選択条件 φ）
(i) A_iθc，A_iθA_j は選択条件である．
(ii) α と β を選択条件としたとき，¬α，α∨β，α∧β は選択条件である．
(iii) (i) と (ii) で定義されるもののみが選択条件である．

選択条件は合成可能です．つまり，リレーション R に対して選択条件 φ を施した結果である σ_φ(R) に対して，新たな選択条件 ψ を施すと，その結果は σ_ψ(σ_φ(R))となりますが，質問変形[3] により，
σ_ψ(σ_φ(R))=σ_ψ∧φ(R) が成立します．したがって，σ_ψ(σ_φ(R))=σ_φ(σ_ψ(R)) や σ_φ(σ_φ(R))=
σ_φ(R) などが成立します．また，選択条件とリレーショナル代数演算との最も基本的な関係は次の通りです．ここに，R, S をリレーション，ψ，φ は述語を表します．

 ●

σ_ψ∨φ(R)=σ_ψ(R)∪σ_φ(R)

 ●

σ_ψ∧φ(R)=σ_ψ(R)∩σ_φ(R)

 ●

σ_¬φ(R)=R－σ_φ(R)

なお，コッドはリレーショナル代数演算として上記のごとく 8 つの演算を導入しましたが，演算の
独立性に着目すると，たとえば，和，差，直積，射影，選択の 5 つはお互いに独立した演算であり，
共通，結合，商やその他の演算をそれらを使って表せることはよく知られていることです．たとえば
次の通りです．

 ●

共通：R∩S=R－(R－S)

 ●

θ-結合：R⨝_AiθBjS=σ_R.AiθS.Bj(R×S)

 ●

自然結合：R⨝S=π_ΩR∪ΩS (_{σR.C1=S.C1∧R.C2=S.C2∧．．．∧R.Cr=S.Cr}(R×S))，ここに
{C₁, C₂, _…, C_r}=Ω_R∩Ω_S

 ●

左外結合：R⟕S= (R⨝S)∪(R –π_ΩR(R⨝S))×{(null, _…, null)}

 ●

右外結合：R⟖S= (R⨝S)∪{(null, _…, null)}×(S –π_ΩS(R⨝S))

 ●

完全外結合：R⟗S= (R⨝S)∪(R –π_ΩR(R⨝S))×{(null, _…, null)}∪{(null, _…, null)}×
(S –π_ΩS(R⨝S))

さらに補足をすると，リレーショナルデータモデルが提案された当初，選択は θ-選択として定義されていました．その定義は次の通りです．

つまり，θ-選択は選択条件 φ の定義 3 の (i) 項の A_iθA_j は選択条件であるという定義から直接導けます．また，上で記しましたが，選択条件は合成可能ですから θ-選択を合成した演算が選択ということになります．したがって，両者をいたずらに区別する必要はなく，特に φ=A_iθA_j を強調したい場合に θ-選択という，と使い分けをすることとします．
結合演算には上記のようにさまざまな結合形態があり，それらを峻別するために最も基本的な結合を θ-結合としたと理解すればよいと思います．他の結合は θ-結合を合成していくことで得られます．

■ Null と 3 値論理

コッドが初めてリレーショナルデータモデルを提案したとき，リレーションの属性が null（空，値がないことを表す）をとることは想定されていませんでした [1]．そこでは，リレーション R(A₁, A₂, _…, A_n) は dom(R)=dom(A₁)×dom(A₂)×・・・×dom(A_n) の有限部分集合と定義されますが，各ドメイン dom(A_i) は単純（simple）である，つまり，integer あるいは文字列からなる集合で，それが null を含むことは想定されていませんでした．したがって，リレーショナル代数演算は 2 値論理に基づいて定義できました．
リレーショナルデータモデルに null が導入されたのは，より多くの意味をリレーショナルデータモデルに取り込もうとレーショナルデータモデルを拡張したコッドの 1979 年の論文で，そこで初めて 3 値論理に基づくリレーショナル代数が導入されました [5]．
一方，ビューの更新可能性を論じるときには，リレーションやビューの属性が null をとらざるを得ない状況が発生します．たとえば，リレーション R(A, B, C)，ここに A は主キー，の属性集合 {A, B} 上の射影ビュー V=π_{{A, B}}(R) はキー保存なので，V に対する挿入は変換可能です（3.2 節【10】項）．たとえば，i=insert (a, b) into V; は R への挿入 T(i)=insert (a, b, null) into R; に変換可能です．つまり，リレーション R に当初は属性が null となるタップルが存在しなかったとしても，いずれはそのようなタップルが存在する可能性があるわけです．
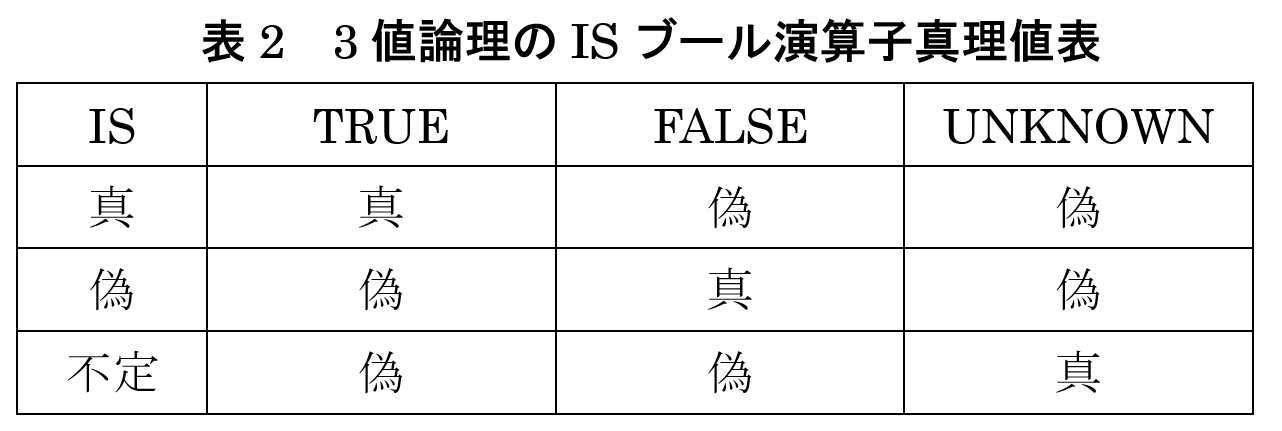
したがって，ビューサポートの理論ではリレーショナル代数演算は 3 値論理を導入した拡張が前提となります．この導入により影響を受ける演算は選択や θ-結合で，それらは推量 θ-選択（maybe θ-selection）や推量 θ-結合（maybe θ-join）の導入に繋がります．定義 3 の (i) 項で与えたようにA_iθc，A_iθA_j は選択条件であるので，これらの述語の値は A_i や A_j が null でなければ真か偽をとりますが，そうでない場合には「不定」（unknown）をとります．たとえば，「2＞3=偽」ですが「2＞null=不定」となります．そうすると，リレーション R(A₁, A₂, _…, A_n) の推量 θ-選択は σ_AiθωAj(R)={t|R(t)∧t[A_i]θ[A_j] IS UNKNOWN} と定義されます．ここで t[A_i]θ[A_j] IS UNKNOWN の真理値は表 2 に示される「3 値論理の IS ブール演算子真理値表」で規定されます．たとえば，属性に null を許容したリレーションを R(A, B, C)={(1, 5, 3), (2, 3, 8), (3, 2, null), (4, null, 6), (5, null, null)} とすれば，
σ_B＞C(R)={(1, 5, 3)} ですが，σ_B＞ωC (R)={(3, 2, null), (4, null, 6), (5, null, null)} となります．なお，
推量 θ-結合は推量 θ-選択を用いて，推量 θ-結合は R⨝_AiθωBjS=σ_R.AiθωS.Bj(R×S) と定義できます [10]．
このように，ビューサポートでは null を導入した 3 値論理に基づいた論理展開が必要なのですが，表 1 のリレーショナル代数演算の選択や θ-結合の定義には推量 θ-選択や推量 θ-結合が陽には表れていません．もちろんそれらを許すように表 1 を拡張できますが，表 1 にそれらを明示していないのは，もっぱら 2 値論理のリレーショナル代数演算の下でビューの更新可能性を論じることで，ビューサポートの議論全体の見通しをよくしようと考えたからです．null を扱わないといけない状況に直面したときには，3 値論理に従って思考してください．たとえば，リレーション R(A₁, A₂, _…, A_n) の属性 A_i と A_j 上の θ-選択ビュー V は 3 値論理では V=σ_AiθAj(R)={t|R(t)∧t[A_i]θ[A_j] IS TRUE} と定義されますが，これは 2 値論理での V=σ_AiθAj(R)={t|R(t)∧t[A_i]θ[A_j]} と同値です．一方，R の属性 A_i と A_j 上の推量 θ-選択ビュー V は V=σ_AiθωAj(R)={t|R(t)∧t[A_i]θ[A_j] IS UNKNOWN} と定義され，3 値論理に従います．より具体的には，上記のリレーションR(A, B, C)={(1, 5, 3), (2, 3, 8), (3, 2, null), (4, null, 6), (5, null, null)} の属性 B と C 上の「推量大なり（＞）選択ビューV」は V=σ_B＞ωC (R)={(3, 2, null), (4, null, 6), (5, null, null)} となりますが，B 上の「推量以下（≦）演算」を使った削除 d=delete σ_B≦ω10 (V) from V; が発行されたとすると，d は T(d)= delete σ_B≦ω10 (R) from R; と基底リレーション R に変換可能で，R から {(4, null, 6), (5, null, null)} が削除され，その結果 V={(3, 2, null)} となり，所望の削除が実現されていることがわかります．このような拡張はバッグ代数についても同様です．

3.1.2 リレーショナル代数表現としてのリレーショナルビュー

 リレーショナルデータベースに対する問合せ（query）はリレーショナル代数表現（relational algebra expression）として記述できますが，ビューは問合せによって定義される仮想的リレーションなので，リレーショナルビューはレーショナル代数表現を使って再帰的に定義することができます．それを定義 4 に与えます．リレーショナル代数演算の独立性から，和，差，直積，射影，選択の 5 つの演算を使ってビューを定義しています．実リレーションとはデータベースに格納されているリレーショナルのことをいいます．なお，本来はリレーショナルビューと書くべきなのですが，ここでは特段の混乱は生じないと考えられるので，単にビューと記しています．
【定義４】（ビュー）

 (1)

実リレーション R はビューである．

 (2)

V₁ と V₂ を和両立なビューとするとき，それらの和 V₁∪V₂ はビューである（和ビュー）．

 (3)

V₁ と V₂ を和両立なビューとするとき，それらの差 V₁－V₂ をはビューである（差ビュー）．

 (4)

V₁ と V₂ をビューとするとき，それらの直積 V₁×V₂ はビューである（直積ビュー）．

 (5)

V をビューとするとき，その射影 πx(V) はビューである（射影ビュー）．

 (6)

V をビューとするとき，その選択 σ_φ(V) はビューである（選択ビュー）．

 (7)

(1)～(6) で定義されるもののみがビューである．

ビューを定義するときに使われる実リレーションをそのビューの基底リレーション（underlying base relation）といいます．基底リレーションを使って (1)～(6) 項のいずれかの演算を 1 度だけ使用して定義されるビューを基本的ビュー（basic view），定義4 の (1)～(6) 項で定義された演算を再帰的に適用して定義されるビューを一般的ビュー（general view）ということにします．この定義に従えば，（定義 4 には陽には出現しなかった）共通ビュー，結合ビュー，商ビュー，外結合ビューなどは一般的ビューとして定義されることになります．ちなみに，R(A, B, C)，S(B, D) をリレーション（アンダーバーは主キーを表す）としたとき，連言問合せ（conjunctive query）として定義されるビュー V=
π_{{R.A, R.B}}(σ_C=c(R)⨝_R.B=S.Bσ_D=d(S)) は一般的ビューの典型です．なお，テーブルにタップルの重複
出現を許している SQL では avg, sum, max, min, count といった集約（aggregation）が有効ですが，リレーションは重複タップルの出現を許していないので SQL ほどの有効性はないと考えて，リレーショナル代数表現としてビューを定義する際には集約関数は特段に考慮していません．

■ ビューと一貫性制約

リレーショナル代数を使ってビューを定義しているということは，リレーショナルデータベースに対する問合せの結果をビューと称し，それらを再帰的にリレーショナル代数演算のオペランドに使用することで，あらゆる問合せの結果をビューとすることができるという意味です．ここで注意しないといけないことは，たとえば，定義 4 の (1) 項より「実リレーション R はビュー V である」と定義できますが，V と R は同一ではなく，SQL の表現を用いれば，問合せ SELECT * FROM R の結果リレーションをビュー V と定義したということです．どういうことかというと，R(A₁, A₂, _…, A_n) としたとき V(A₁, A₂, …, A_n) と書けて，インスタンスとしての R と V は同一ではあるものの，R をインスタンスとするリレーションスキーマ R(A₁, A₂, _…, A_n) に定義されている一貫性制約は V では定義されていないということです．あくまで，V は SQL で表現すれば CREATE VIEW V AS SELECT * FROM R と定義されるように，単に SELECT * FROM R の結果リレーションでしかないからです．実リレーションとビューとのこの差異は大きいと認識するべきで，すでに関連した議論を 2.3 節 (d) 項で行っていますが，ビューはあくまで更新の窓口であって，それが更新可能である場合，その更新がデータベースの一貫性制約に抵触するかしないかの検証はそのビューを定義するために使われた基底リレーションで行うということです．なお，更新時の一貫性制約の検証はビューに特有ではなく，一般にリレーショナルデータベースの実リレーションを更新した場合でも必ず行われないといけないわけで，これがビューの更新可能性を規定した定義1の条件から (d) 項を外した理由となったことは前述の通りです．
以下，実リレーション R がビュー V であることを V=R と表示したり，実リレーション R と S の和ビュー V を V=R∪Sと 表示したりしますが，「=」（等号）の意味は上記のごとく，単に右辺での問合せの結果リレーションを左辺（＝ビュー）としたということで，リレーションスキーマとしての同一性を表現しているものではありません．この議論はバッグビューに対しても全く同様に成立します．

3.2 基本的リレーショナルビューの更新可能性（スキーマレベル）

 表 3 に「基本的リレーショナルビューの更新可能性（スキーマレベル）」の結果を示します（ここでは，コッドの定義した 8 つのリレーショナル代数演算で定義されるビューを基本的ビューとしています）．行列値の 〇 は更新可能，× は更新不可能を表します．†はキー保存という条件を表しています．

以下，表 3 が得られた論拠を示します．要点は，ビューの更新可能性をスキーマレベルで論じているので，更新可能であることを示すにはすべてのインスタンスに対して更新可能であることを示す必要があること，一方で更新不可能を示すにはそのようなインスタンスと更新の組合せを 1 例示せばよいということです．

【1】和ビューは削除可能

 R と S を和両立なリレーション，V=R∪S を和ビューとする．
V に対して削除 d=deleteσ_φ(V) from V; が発行されたとする．ここに φ は探索条件である．削除の定義は V←V－σ_φ(V) なので，この削除を表す論理式は次の通りである．
∀t(t∈σ_φ(V)⇒¬V(t))
つまり，φ(t)=真となる V のタップル，つまり σ_φ(V) のタップル，は（削除後は）V のタップルであってはいけないと言っている．
一方，V=R∪S なので t∈σ_φ(V)⇔t∈σ_φ(R∪S)⇔t∈σ_φ(R)∨t∈σ_φ(S) である．したがって，
t∉σ_φ(V)⇔t∉σ_φ(R)∧t∉σ_φ(S) である．
つまり，「d を実現するためには，R から探索条件 φ を満たすタップルをすべて削除しかつ S からも探索条件 φ を満たすタップルをすべて削除することが必要かつ十分である」と言っている．このとき，(R－σ_φ(R))∪(S－σ_φ(S))=(R∪S)－(σ_φ(R)∪σ_φ(S)) =V－σ_φ(R∪S)=V－σ_φ(V) が成り立つ．したがって，d を実現するための必要かつ十分条件は d を T(d) に変換することである．
T(d)=begin; deleteσ_φ(R) from R; deleteσ_φ(S) from S; end;
このことは，特定のR，S，φ に依存することなく成立するので，「和ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

【例題１】R(A, B), S(A, B), dom(A)=dom(B)={i|Integer(i)}, R={(1, 1), (2, 2)}, S={(2, 2), (3, 3)}, V=R∪S={(1, 1), (2, 2), (3, 3)}, φ=(A=2∧B=2) とする．このとき，σ_φ(V)={(2, 2)} なので，V－σ_φ(V)={(1, 1), (3, 3)} であり, 一方，R－σ_φ(R)={(1, 1)}, S－σ_φ(S)={(3, 3)} なので (R－σ_φ(R))∪(S－σ_φ(S))= {(1, 1)}∪{(3, 3)}={(1, 1), (3, 3)} となり，d=deleteσ_φ(V) from V; が T(d)=begin; deleteσ_φ(R) from R; deleteσ_φ(S) from S; end; により実現できていることが確認できる．

【2】和ビューは挿入不可能

 和ビューは挿入不可能であるインスタンスレベルの反例を一つ示せばよい．たとえば，和両立な 2 つのリレーションを R(A, B)=∅, S(A, B)= ∅（ここに ∅ は空集合を表す）とすると，V=R∪S=∅ である．このとき，V に対する挿入 i=insert {(1, 1)} into V; が発行されたとする．挿入の定義は V←V∪{(1, 1)} なので，この挿入を表す論理式は次の通りである．
∀t(t∈{(1, 1)}⇒V(t))
一方，∀t(V(t)⇔R(t)∨S(t)) なので，i を実現する変換 T は 3 つ存在することが分かる．
T₁(i)= insert {(1, 1)} into R;
T₂(i)= insert {(1, 1)} into S;
T₃(i)= begin; insert {(1, 1)} into R; insert {(1, 1)} into S; end;
しかしながら，これら 3 つの変換の存在は変換の一意性に反するので，定義 1 より V への挿入 i は変換不可能である．したがって，「和ビューは挿入不可能である」という命題がスキーマレベルで成立する．

したがって，「和ビューは書換不可能である」という命題がスキーマレベルで成立する．

【3】差ビューは削除不可能

 差ビューは削除不可能であるインスタンスレベルの反例を一つ示せばよい．たとえば，和両立な 2 つのリレーションを R(A, B)={(1, 1), (2, 2)}, S(A, B)={(1, 1), (3, 3)} とする．このとき，差ビュー V=R－S={(2, 2)} である．
そこで，V に対する削除 d=deleteσ_φ(V) from V; ここに φ=(A=2∧B=2)，つまり σ_φ(V)= {(2, 2)}，が発行されたとする．
削除の定義は V←V－σ_φ(V) なので，この削除を表す論理式は次の通りである．
∀t(t∈σ_φ(V)⇒¬V(t))
一方，¬V(t)⇔t∉V⇔t∉(R－S)⇔t∉R∨t∈S である．
したがって，d を実現する変換 T が 3 つ存在することが分かる．
T₁(d)= delete {(2, 2)} from R;
T₂(d)= insert {(2, 2)} into S;
T₃(d)= begin; delete {(2, 2)} from R; insert {(2, 2)} into S; end;
この 3 つの変換の存在は変換の一意性に反するので，定義 1 より V への削除 d は変換不可能である．したがって，「差ビューは削除不可能である」という命題がスキーマレベルで成立する．

【4】差ビューは挿入可能

 R と S を和両立なリレーション，V=R－S を差ビューとする．
V に対して挿入 i=insert X into V;　ここに X⊆dom(R)，が発行されたとする．挿入の定義は V←V∪X なので，この挿入を表す論理式は次の通りである．
∀t(X(t)⇒V(t))
一方，差ビューの定義より，∀t(V(t)⇔R(t)∧¬S(t)) である．
したがって，挿入に関して次に示す論理式を得る．
∀t(X(t)⇒R(t)∧¬S(t))
つまり，「V に X を挿入するためには，R に X を挿入し S から X を削除しなさい」と言っている．このとき，(R∪X)－(S－X)=(R－S)∪X=V∪X が成り立つ．したがって，i を実現するための必要かつ十分条件は i を T(i) に変換することである．
T(i)=begin; insert X into R; delete X from S; end;
このことは，特定の R，S，X に依存することなく成立するので，「差ビューは挿入可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「差ビューは書換不可能である」という命題がスキーマレベルで成立する．

【5】共通ビューは削除不可能

 和両立なリレーション R と S の共通は R∩S=R－(R－S) であるので，一般的ビューとなる「差ビューは削除不可能である」という命題がスキーマレベルで成立しているので，「共通ビューは削除不可能である」という命題がスキーマレベルで成立する．

【6】共通ビューは挿入可能

 R と S を和両立なリレーション，V=R∩S を共通ビューとするとき，それは次のように定義される．
∀t(V(t)⇔(R(t)∧S(t)))
そこで，V に対して挿入 i=insert X into V; ここに X⊆dom(R) が発行されたとする．挿入の定義はV←V∪Xなので，この挿入を表す論理式は次の通りである．
∀t(X(t)⇒V(t))
したがって，挿入に関して次に示す論理式を得る．
∀t(X(t)⇒(R(t)∧S(t)))
つまり，「V に X を挿入するためには，R に X を挿入しかつ S に X を挿入しなさい」と言っている．このとき，(R∪X)∩(S∪X)=(R∩S)∪X=V∪X である．したがって，i を実現するための必要かつ十分条件は i を T(i) に変換することである．
T(i)=begin; insert X into R; insert X into S; end;
このことは，特定の R，S，X に依存することなく成立するので，「共通ビューは挿入可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「共通ビューは書換不可能である」という命題がスキーマレベルで成立する．

【7】直積ビューは削除不可能

 インスタンスレベルでの反例を一つ示す．2 つのリレーションを R(A, B)={(1, 1)}, S(C, D)={(1, 1)}，直積ビューを V=R×S={(1, 1, 1, 1)} とする．このとき，V に対して削除 d=delete σ_φ(V) from V; ここに φ=(A=1∧B=1∧C=1∧D=1) が発行されたとする．
削除の定義は V←V－σ_φ(V) なので，この削除を表す論理式は次の通りである．
∀t(t∈σ_φ(V)⇒¬V(t))
V=R×S={u*v|u∈R∧v∈S} なので，¬V(t)⇔t∉(R×S)⇔u∉R∨v∉S，ここに t=u*v とする，である．
一方，σ_φ(V)⇔σ_φ(R×S)⇔σ_φ1(R)×σ_φ2(S)，ここに φ はΩ_R×S=Ω_R×Ω_S 上の選択条件で，φ₁=φ|Ω_r と φ₂=φ|Ω_S はそれぞれ φ を Ω_R とΩ_S 上に制限した探索条件を表す．この例では φ₁=(A=1∧B=1)，φ₂=(C=1∧D=1) である．
したがって，d を実現する変換 T が 3 つ存在することが分かる．
T₁(d)= delete σ_φ1(R) from R; ここに φ₁=(A=1∧B=1)
T₂(d)= delete σ_φ2(S) from S; ここに φ₂=(C=1∧D=1)
T₃(d)= begin; delete σ_φ1(R) from R; delete σ_φ2(S) from S; end;
これは，変換の一意性に反するので，定義 1 より V への削除 d は変換不可能である．したがって，「直積ビューは削除不可能である」という命題がスキーマレベルで成立する．

【8】直積ビューは挿入不可能

 インスタンスレベルで反例を一つ示す．2 つのリレーションを R(A, B)={(1, 1)}, S(C, D)={(1, 1)} とする．このとき，V=R×S={(1, 1, 1, 1)} を直積ビューとする．このとき，V に対して挿入 i=insert {(2, 2, 2, 2) } into V; が発行されたとする．このとき，i を実現するためには R に (2, 2) を挿入し S には (2, 2) を挿入しないといけない．しかしながら，それにより V={(1, 1, 1, 1), (2, 2, 2, 2), (1, 1, 2, 2), (2, 2, 1, 1) } となり副作用が生じる．したがって，「直積ビューは挿入不可能である」という命題がスキーマレベルで成立する．

したがって，「直積ビューは書換不可能である」という命題がスキーマレベルで成立する．

【9】射影ビューは削除可能

 リレーション R の属性集合 X（X⊆Ω_R）上の射影ビューを V=π_X(R) とする．V に対して削除 d=delete σ_φ(V) from V; が発行されたとする． ここに選択条件 φ は dom(V)（=dom(X)）の元を引数とする述語であるが，X⊆Ω_R なのでdom(R) の元を引数とする述語ともなっている．
このとき，σ_φ(V)=σ_φ(π_X(R))= π_X(σ_φ(R)) である．
d の定義は V←V－σ_φ(V) であるので，V－σ_φ(V)= π_X(R)－π_X(σ_φ(R))=π_X(R－σ_φ(R)) となる．
つまり，d を実現するためには，「R から σ_φ(R) を削除して，その結果を X 上で射影しなさい」と言っている．このとき，φ は dom(R) の元を引数とする述語ともなっているので，
π_X(R－σ_φ(R))=π_X(R)－π_X (σ_φ(R))=π_X(R)－σ_φ(π_X(R))=V－σ_φ(V) が成立する．
したがって，d が変換可能であるための必要かつ十分条件は d を T(d) に変換することである．
T(d)=deleteσ_φ(R) from R;
このことは R と X と φ がどのような場合でも成り立つ．よって，「射影ビューは削除可能である」という命題はスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

【例題２】R(A, B)={(1, 1), (1, 2), (2, 1)}, V=π_{B}(R)={(1), (2)} とし, V に対して削除 d=delete _σB=1∨B=3(V) from V; が発行されたとする．T(d)=delete _σB=1∨B=3(R) from R; に変換されるが，T(d) により B=1 の R のタップル (1, 1) と (2, 1) は R から削除される．B=3 のタップルは R に存在しないので R から削除されるタップルはない．したがって，R={(1, 2)} となるから，π_{B}(R)={(2)}と 所望の結果となっている．

【10】射影ビューはキー保存ならば挿入可能
リレーション R の属性集合 X⊆Ω_R 上の射影ビューを V=π_X(R) とするとき，射影ビュー V がキー保存（key preservation）であるとは，X がリレーション R の主キー K を含むときをいう．
そこで，リレーション R の属性集合 X 上の射影ビューを V=π_X(R) とすると，V の定義から次が成立する．
∀u(V(u)⇔∃t(R(t)∧u=t[X]))
V に対して挿入 i=insert W into V; ここに W⊆dom(V) が発行されたとする．この挿入を表す論理式は次の通りである．
∀v(W(v)⇒V(v))
したがって，次が成立する．
∀v(W(v)⇒∃t(R(t)∧v=t[X]))
このとき，挿入 i=insert W into V; の R への変換 T を次のように定義する．
T(i)=insert W～ into R;
ここに W～ は W から次のように定義されるタップル w~ の集合で，w∈W とした時，タップル w~ は次のように定義される．
w~[X]=w∧w~[Ω_R－X]=(null, null, _…, null)
さて，射影ビュー V がキー保存であるとすると，K を R の主キーとしたとき，K⊆X であるので，∀w, w’(W(w)∧W(w’)∧(w[K]≠w’[K]⇒w≠w’))が成立する．加えて，K は（候補キーではなく）主キーなので，キー制約からその属性が null をとることはないから，W と W～ の間には w↔w~ という 1 対 1 の対応が成立する．
このとき，π_X(R∪W～)=π_X(R)∪π_X(W～)=π_X(R)∪W=V∪W が成立するので，i を実現するための必要かつ十分条件は i を T(i) に変換することであることが分かる．
T(i)=insert W～ into R;
したがって，「射影ビューはキー保存であれば挿入可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「射影ビューはキー保存ならば書換可能である」という命題がスキーマレベルで成立する．

なお，「キー保存」という条件自体は属性集合 X が主キー K を含んでいるかどうかという判定なのでスキーマレベルの検証であるので，定義 1 の条件 (a)～(c) をクリアして「射影ビューはキー保存ならば挿入可能である」という命題はスキーマレベルで成立することとなった．
ただし，変換可能ならば基底リレーション R に W～ が挿入されることになるが，その挿入が R のキー制約に抵触するのかしないのかのチェックが必ず必要となってくることに注意したい．

【例題３】R(A, B)={(1, 1), (2, 2), (3, 3)}, V=π_{A}(R)={(1), (2), (3)}, i=insert {(4)} into V; が発行されたとする．i の変換 T(i)= insert {(4, null)} into R; とする．その結果，R(A, B)={(1, 1), (2, 2), (3, 3), (4, null)} となり，改めて π_{A}(R)= {(1), (2), (3), (4)} となりなって，所望の挿入が実現していることがわかる．

【11】選択ビューは削除可能
リレーション R の選択ビューを V=σ_φ(R) とする．V に対して削除 d=deleteσ_ψ(V) from V; が発行されたとする．d の定義は V←V－σ_φ(V) であるが，V－σ_φ(V)=σ_φ(R)－σ_ψ(σ_φ(R))=σ_φ(R)－σ_φ(σ_ψ(R))=σ_φ(R－σ_ψ(R)) となる．
つまり，d を実現するためには，「R から σ_ψ(R) を削除して，その結果に φ を施しなさい」，つまり，d を T(d) に変換しなさいと言っている．
T(d)=deleteσ_ψ(R) from R;
このとき，上記のごとく σ_φ (R－σ_ψ(R))= V－σ_φ(V) であるので，この変換は d が変換可能であるための必要かつ十分条件になっている．この性質は R と φ と ψ がどのような場合でも成り立つので，「選択ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

【例題４】社員(社員番号，給与)={(1, 10), (2, 20), (3, 30)} を実リレーション，ビューを貧乏社員=σ_給与≦20(社員)={(1, 10), (2, 20)} とし，削除 d=delete σ_給与≧10 (貧乏社員) from 貧乏社員; が発行されたとする．d は変換可能で次の通りである．
T(d)=deleteσ_{給与≧10∧給与≦20}(社員) from 社員;

【12】選択ビューは挿入可能
リレーション R の選択ビューを V=σ_φ(R)とする．V に対して挿入 i=insert X into V; が発行されたとする．i の定義は V←V∪X なので，この挿入を表す論理式は次の通りである．
∀t(X(t)⇒V(t))
一方，選択ビューの定義より，∀t(V(t)⇔R(t)∧_φ(t)) である．したがって，次に示す論理式を得る．
∀t(X(t)⇒(R(t)∧φ(t)))
ところで，X⊆dom(V)=σ_φ(dom(R)) なので，∀t(X(t)⇒_φ(t))，つまり ∀t(t∉X(t)∨_φ(t)) が成立している．したがって，
∀t(X(t)⇒(R(t)∧φ(t)))⇔∀t(t∉X(t)∨(R(t)∧_φ(t)))⇔∀t((t∉X(t)∨(R(t))∧(t∉X(t)∨_φ(t)))⇔∀t(t∉X(t)∨(R(t)) ⇔∀t(X(t)⇒R(t)) となる．
つまり，「iを実現するためには，R に X を挿入しなさい」と言っている．このとき，X⊆σ_φ(dom(R))なので σ_φ(X)=X となり，σ_φ(R∪X) =σ_φ(R)∪σ_φ(X)=V∪X である．したがって，i を実現するための必要かつ十分条件は iを T(i) に変換することである．
T(i)= insert X into R;
このことは，特定の R，φ，X に依存することなく成立するので，「選択ビューは挿入可能」であるという命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「選択ビューは書換可能である」という命題がスキーマレベルで成立する．

【例題５】社員(社員番号，給与)={(1, 10), (2, 20), (3, 30)} を実リレーション，貧乏社員=σ_給与≦20(社員)={(1, 10), (2, 20)} をビューとし，挿入 i=insert {(100, 10), (101, 15)} into 貧乏社員; が発行されたとする．i は変換可能で，その変換は次の通りである．
T(i)=insert {(100, 10), (101, 15)} into社員;

【13】結合ビューや商ビューは共に削除不可能，挿入不可能，書換不可能
これらを定義するためには直積演算が使われるので，それらの更新可能性に則して，共にスキーマレベルで削除不可能，挿入不可能，書換不可能である．

3.3 一般的リレーショナルビューの更新可能性（スキーマレベル）

 一般にリレーショナルビューはリレーショナル代数演算を「再帰的」に適用して定義されます．このようなビューを「一般的リレーショナルビュー」といいますが，そのようなビューの更新可能性はそのビュー定義に使われたリレーショナル代数演算で定義される中間ビューの更新可能性に依存することになります（このことは，後述する一般的バッグビューについても同様です）．
ここではリレーショナルデータベースで最も典型的であるといわれている連言問合せ（conjunctive query）で定義されるビューを例として説明します．
【例題６】（一般的リレーショナルビューの更新可能性判定）
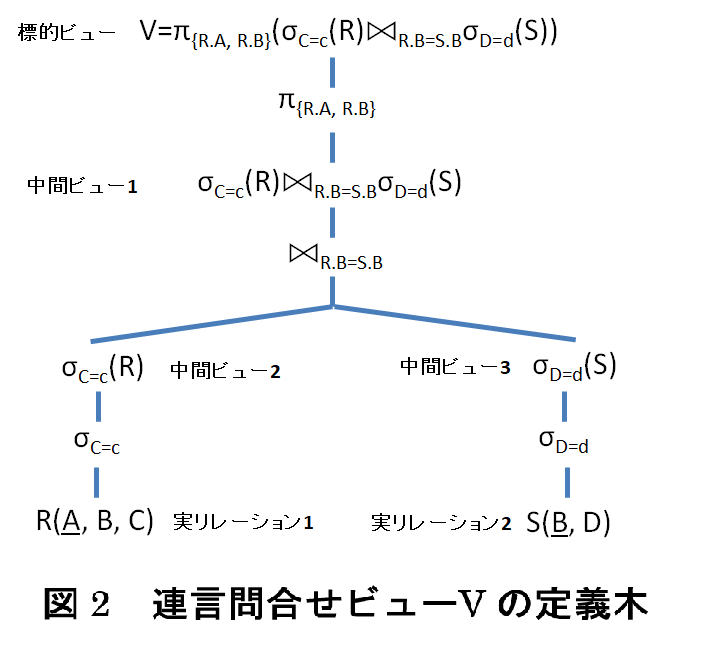
R(A, B, C)，S(B, D) をリレーション（アンダーバーは主キーを表す），V=π_{{R.A, R.B}}(σ_C=c(R)
⨝_R.B=S.Bσ_D=d(S)) を連言問合せビュー定義とする．このビューの定義木（＝構文解析木）を図 2 に示す．
このとき，V へ更新 u が発行されると，V=π_{{R.A, R.B}} 中間ビュー₁ なので，射影ビューに対する u の変換可能性をチェックする．表 3 を参照すると（table lookup），u が削除ならば変換可能，u が挿入ならばキー保存という条件付きで変換可能であることを知る．ともに，（挿入には条件が付くが）変換可能なので，V への更新 u の変換可能性は，中間ビュー₁ に対する更新の変換可能性のチェック結果に依ることとなる．ところが，中間ビュー₁ は結合ビューである．そこで，再び表 3 を参照すると，結合ビューは削除不可能，挿入不可能，書換不可能であることを知る．したがって，u は押し並べて変換不可能であることを知る．この時点で，ビュー V への更新 u が変換不可能であると判定される．

このように，一般的リレーショナルビューの更新可能性はそのビューの定義木をトップダウンに，たとえば幅優先探索（breadth first）で走査しながら，ノードごとでその更新可能性を表 3「基本的リレーショナルビューの更新可能性（スキーマレベル）」に参照していけば，その更新可能性をスキーマレベルで検証することができます．

4. バッグビューの更新可能性（スキーマレベル）

4.1 バッグビューの定義

4.1.1 バッグ

 SQL のテーブルはリレーションと異なりタップルの重複出現を許します．タップルの重複出現を許すことで問合せの結果から重複タップルを削除する手間が省けるので（つまりソートや突合せなどの処理を省ける），問合せ処理がリレーションの場合に比べて高速になります．また，タップルの重複出現を許容することで集約関数を駆使できるという利点もあります．反面，SQL のテーブルを格納しておくためにはリレーションに比べて余計に記憶領域を必要とすることは明らかです．
さて，一般に元（element）の重複出現を許す元の集まりをマルチ集合（multiset）あるいはバッグ（bag）といいます．数学ではマルチ集合，SQL ではバッグを用いることが多いので本稿ではバッグとします．タップルの重複出現を許さないリレーションとそれを許すバッグではデータの表現・操作・管理などで違いを生じますが，それはリレーショナルデータモデルは集合意味論（set semantics）に立脚し，SQL はバッグ意味論（bag semantics）に立脚しているからだと表現します．リレーショナルデータモデルでリレーショナル代数（relational algebra）が定義されたと同様に，バッグに対してはバッグ代数（bag algebra）が定義されます [8]．リレーショナル代数表現と同様にバッグ代数表現（bag algebra expression）を定義でき，リレーショナルビューがリレーショナル代数表現で定義されたのと同様に，バッグビュー（bag view）はバッグ代数表現として定義されます．まずはバッグを定義することから始めます．
【定義５】（バッグ）

 バッグ R(A₁, A₂, _…, A_n) は潜在リレーション（concealed relation）R(A₁, A₂, _…, A_n)と重複度関数 m: dom(R)→Z⁺（Z⁺ は正の整数）の組である．ここに dom(R)=dom(A₁)×dom(A₂)×・・・×dom(A_n)とする．

つまり，バッグは R(A₁, A₂, _…, A_n)=(R(A₁, A₂, _…, An), m) と定義されるということです．たとえば，バッグ R(A₁, A₂, _…, A_n) の潜在リレーションを R(A₁, A₂, _…, A_n)= {t₁, t₂, _…, t_p}，重複度関数を m(t_i)=k_i（k_i≧1）とするとき，バッグ R(A₁, A₂, _…, A_n)={t₁(k₁), t₂(k₂), _…, t_p(k_p)} となります．ここに t_i(k_i) はタップル t_i が丁度 k_i 本あることを表すための記法で，k_i はバッグ R 中に生起するタップル t_i の重複度（multiplicity）です．t(k)∈R で重複度 k のタップル t がバッグ R の元であることを表すことにすると，t(k)∈R⇔t∈R∧k=m(t) ということです．バッグ R(A₁, A₂, _…, A_n) ={t₁(k₁), t₂(k₂), _…, t_p(k_p)} は (∀i=1,_..,p)(k_i=1) のときリレーション(＝集合)です．k_i=1 のとき，t_i(1) と書かずに，単に t_i と書くことも多く，また t_i(0) は t_i が存在していないことを意味します．
バッグ R(A₁, A₂, _…, A_n) のドメイン dom(R) は次のように定義されます．dom(R)=dom(R)×
{k|PositiveInteger(k)}=dom(A₁)×dom(A₂)×・・・×dom(A_n)×{k|PositiveInteger(k)}，ここに
PositiveInteger(k) は k が正整数であるとき真となる命題です．ちなみに，(a₁, a₂, _…, a_n, k)∈
dom(R)⇔(a₁, a₂, _…, a_n)(k)∈R と解釈します．

■ 潜在キーと潜在キー制約

バッグはリレーションと違って重複タップルの出現を許すので，バッグの全属性の組をとってきてもタップルの一意識別能力はなく，したがってリレーションのキー（key）に相当する概念はありません．しかしながら，バッグ　R(A₁, A₂, _…, A_n) を定義するために潜在リレーション R(A₁, A₂, _…, A_n) を導入しましたが，R は正真正銘のリレーションなので，R にはキーが存在します．そこで，R のキーを K とし，K をバッグ R の潜在キー（concealed key）と呼ぶことにします．リレーションの主キーと候補キーに対応して潜在主キーと潜在候補キーが定義できます．
潜在キーは一見無秩序に重複タップルの出現を許しているように見えるバッグに「秩序」をもたらしていることになります．換言すれば，潜在キーが K であるバッグ R={t₁(k₁), t₂(k₂), _…, t_p(k_p)} に重複行除去（δ）を施して得られるリレーション δ(R)={t₁, t₂, _…, t_p} のキーは K なので次が成り立ちます．
∀t, t’(t∈δ(R)∧t’∈δ(R)∧t[K]=t’[K]⇒t=t’)
つまり，バッグで重複して出現しているタップル同士のキー値が等しいならばタップルとしては同一だということになります．マルチ集合論では「重複元の識別不可能性」という原理が知られていますが [9]，上記はその原理のデータベース的解釈といえます．
したがって，たとえば，潜在リレーションを社員(社員番号，氏名，所属，給与)，ここに社員番号が主キー，とするバッグ社員(社員番号，氏名，所属，給与) に (007, 山田太郎，K55，50) というタップルは何本出現しても構いませんが，たとえば，(007, 佐藤一郎，K41，50) というタップルがバッグ社員に (007, 山田太郎，K55，50) と共に出現するということはない，ということです．この制約を潜在キー制約（concealed key constraint）と呼ぶことにしますが，これはリレーションでのキー制約に相当する概念で，バッグあるいはバッグビュー更新時の一貫性制約の一つになります．

4.1.2 バッグ代数

 バッグのデータ操作言語であるバッグ代数を定義しますが，以下に示す演算からなります．
【定義６】（バッグ代数）

 一般に，R(A₁, A₂, _…, A_n)={t₁(k₁), t₂(k₂), _…, t_p(k_p)} とS(B₁, B₂, _…, B_m)={u₁(ℓ₁), u₂(ℓ₂), _…, u_q(ℓ_q)} をバッグとするとき，バッグ代数は次に示す演算子からなる．加法和（additive union），モーナス（monus），共通を定義するにあたり R と S は和両立とする．
● 重複行除去（δ）
● 加法和（⨄），モーナス（∸），共通（∩）
● 直積（×）
● 射影（π_X(R)，ここに Ｘ⊆Ω_R）
● 選択（σ_φ (R)，ここに φ は dom(R) 上の選択条件）
● θ-結合（R⨝_AiθBjS，ここに R.A_i と S.B_j は θ-比較可能）

これらの演算子の定義を表 4 で与えます．

補足すれば，バッグ代数に特有な演算として，重複行削除演算（δ），モーナス（∸），加法和（⨄）をあげられます．モーナス（∸）はリレーショナル代数演算の差（－）に対応した演算ですが，タップルの重複度を考慮しています．マルチ集合論では和には加法和とは別に最大和（maximum union，∪）を定義することもできます．その定義は R∪S={t(k)|∃t(k_i)∈R∧∃t(ℓ_j)∈S∧k= max(k_i, ℓ_j)} で，リレーショナル代数の和（∪）はバッグ代数の最大和と両立する演算です．しかしながら，
一般にタップルの重複出現を許す SQL のテーブルの UNION ALLを念頭においている和は加法和です．
SQL との対応付けをすると，重複行削除演算は SQL の SELECT DISTINCT * FROM R に相当します．加法和，モーナス，共通はそれぞれ SQL の UNION ALL，EXCEPT ALL，INTERSECT ALL に相当します．直積，選択，射影，θ-結合の演算結果から重複行は削除されず SQL の SELECT ALL の意味を持っています．上記の演算はお互いに独立ではなく，たとえば，重複行除去，加法和，差，直積，射影，選択の 6 つの演算は互いに独立です．独立でない演算子を許容しているのはその有用性によります．
なお，R, S をバッグ，ψ, φ を述語としたとき，次の性質が成り立ちます [8]．このような性質はバッグ代数で成り立つので，リレーショナル代数でも成り立ちます．
● σ_ψ∨φ(R)=σ_ψ(R) ⨄σ_φ(R)
● σ_ψ∧φ(R)=σ_ψ(R)∩σ_φ(R)
● σ_¬φ(R)=R∸σ_φ(R)
● δ(σ_φ(R))=σ_φ(δ(R))

バッグ代数でもバッグのタップルの属性が null をとることがありうるので，バッグ代数演算もリレーショナル代数の時と同じように（3.1.1 項），3 値論理に拡張されて，推量 θ-選択や推量 θ-結合が定義できます．

4.1.3 バッグ代数表現としてのバッグビュー

 リレーショナルデータベースに対する問合せがリレーショナル代数表現として記述できたのと同様に，バッグデータベースに対する問合せはバッグ代数表現として記述できます．したがって，定義 4 でリレーショナルビューを定義したのと同様に，バッグビューはバッグ代数表現として次のように定義できます．データベースに格納されているバッグを実バッグといいます．
【定義７】（バッグビュー）

 (1)

実バッグはバッグビューである．

 (2)

V をバッグビューとし，δを重複行除去とするとき，δ(V) はバッグビューである（重複行除去ビュー）．

 (3)

V₁ と V₂ を和両立なバッグビューとするとき，それらの加法和 V₁⨄V₂ はバッグビューである（加法和ビュー）．

 (4)

V₁ と V₂ を和両立なバッグビューとするとき，それらのモーナス V₁∸V₂ はバッグビューである（モーナスビュー）．

 (5)

V₁ と V₂ をバッグビューとするとき，それらの直積 V₁×V₂ はバッグビューである（バッグ直積ビュー）．

 (6)

V をバッグビューとするとき，その射影 π_X(V) はバッグビューである（バッグ射影ビュー）．

 (7)

V をバッグビューとするとき，その選択 σ_φ(V) はバッグビューである（バッグ選択ビュー）．

 (8)

(1)～(6) で定義されるもののみがバッグビューである．

基本的バッグビューと一般的バッグビューという用語も基本的リレーショナルビューと一般的リレーショナルビューに準じて使用します．以下，特に混乱が生じないと考えられる場合にはバッグビューを単にビューと記すこともあります．

4.2 バッグビューの更新

 バッグビュー V に対する削除や挿入に対する形式や考え方はリレーショナルビューに対する削除や挿入と基本的には同一ですが，削除では差に代わりモーナスが，挿入では和に代わり加法和がその定義に用いられるところが異なります．書換を削除と挿入の系列と定義することや注意点はリレーショナルビューに対する場合と同様です．
削除（d）：deleteσ_φ(V) from V; ここに φ は dom(V) の元を引数とする述語である．
挿入（i）：insert X into V; ここに X⊆dom(V) とする．
● 削除の定義は V←V∸σ_φ(V) です．モーナスが使われているとことに注意します．
● 挿入の定義は V←V⨄X です．加法和が使われているとことに注意します．

ここで，バッグビューのドメインについて補足をします．

■ バッグビューのドメインについて

4.1.1 項で，バッグ R(A₁, A₂, _…, A_n) のドメインは dom(R)=dom(A₁)×dom(A₂)×・・・×dom(A_n)×{k|PositiveInteger(k)} と定義されました．バッグビューのドメインもその延長線上にありますが，（リレーショナルビューのときと同様に）ビュー定義が勘案されます．つまり，バッグビューを V(A_1’, A_2’, _…, A_r’) としたとき，V のドメインは一般には dom(V)=dom(A_1’)×dom(A_2’)×・・・×dom(A_r’)×{k|PositiveInteger(k)} とはならず，ビュー定義を満たすその部分集合になります．幾つか例題で見ていくと次の通りです．
まず，バッグ R(A₁, A₂, _…, A_n) の重複行削除ビュー V=δ(R) のドメインは dom(V)= dom(A₁)×
dom(A₂)×・・・×dom(A_n)×{1} です．R と S を和両立とするとき加法和ビュー V=R⨄S やモーナスビュー V=R∸S のドメインは dom(V)=dom(R)×{k|PositiveInteger(k)} です．バッグ R と S の直積ビュー V=R×S のドメインは dom(V)=dom(R)×dom(S)×{k|PositiveInteger(k)} です．バッグ R(A₁, A₂, _…, A_n) の属性集合 X（⊆Ω_R），ここに Ω_R={A₁, A₂, _…, A_n}，上の射影ビュー V=π_X(R) のドメインは，X={A_1’, A_2’, _…, A_r’}，ここに 1≦1’≦2’≦…≦r’≦n，として dom(V)=dom(A_1’)×dom(A_2’)×･･･×dom(A_r’)×{k|PositiveInteger(k)} となります．バッグ R(A, B) のバッグ選択ビューを V=σ_B≦b(R) としたとき，dom(V)=dom(A)×σ_B≦b(dom(B))×{k|PositiveInteger(k)} となります．バッグ R(A, B) と S(B,C) の等結合ビュー V(A, R.B, S.B, C)=R⨝_R.B=S.BS のドメインは dom(V)=σ_R.B=S.B(dom(A)×
dom(R.B)×dom(S.B)×dom(C))×{k|PositiveInteger(k)} となります．このようにビューのドメインはいずれもビュー定義が勘案されて定義されます．なお，クライアントにはビューの定義を考慮したうえでそれに抵触しない挿入を発行しなければならないという負担がかかることはリレーショナルビューの場合と同じです．

4.3 基本的バッグビューの更新可能性（スキーマレベル）

 リレーショナルビューが集合意味論に立脚し，バッグビューはバッグ意味論に立脚している点は異なりますが，ビューの更新可能性は定義 1 で与えた通りです．つまり，バッグビュー V への更新 u は，(a) 一意で，(b) 副作用がなく，(c) 余計な更新がない変換 T が存在するとき更新可能であること定義されます．ただ，上述のように，削除にはモーナスが，挿入には加法和が用いられるところが異なります．また，バッグにはそれを定義するための潜在リレーションが存在する点もバッグビューの更新可能性に影響を与えます．なお，本稿ではスキーマレベルでビューの更新可能性を論じているので，リレーショナルビューの場合と同様な理由で，定義 1 の条件 (d) は不問に付しています．

さて，基本的バッグビューの更新可能性（スキーマレベル）をリレーショナル代数の場合と同様なアプローチで解明していきますが，ここで大事なことは次の命題が成立することです．

「リレーション（＝集合）はバッグの特殊な場合なので，バッグで成り立つ性質はリレーションでも成り立つが，リレーションで成り立つ性質が必ずしもバッグで成り立つとは限らない」

したがって，表 3 で〇（更新可能）となっている場合でも，それはリレーショナルビューに対する結果なので，それに対応するバッグ代数でのビューの更新可能性がまた〇になるかどうかは分かりません．一方，表3で×（更新不可能）となっている性質がバッグビューで〇となることはないわけですから，バッグビューの更新可能性はリレーショナルビューのそれに比べて限定的となります．
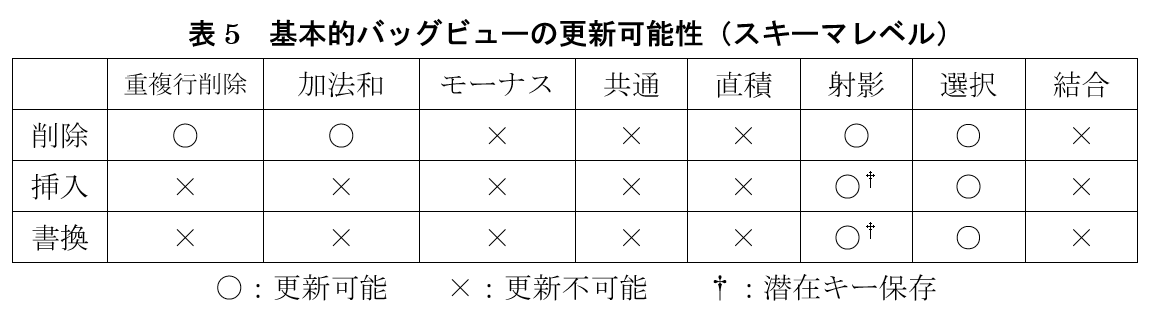
以下，表 5 にバッグビューの更新可能性を検証した結果を示すと共に，その論拠を示します．

【1】重複行削除ビューは削除可能

 一般にバッグ R={t₁(k₁), t₂(k₂), _…, t_p(k_p)} の重複行除去ビュー δ(R)={t₁, t₂, _…, t_p} に対して，削除 d=delete σ_φ(δ(R)) from δ(R); が発行されたとする．
そこで，σ_φ(δ(R)) ={t_1’, t_2’, _…, t_q’}，1≦1’＜2’＜_…＜q’≦pとするとき，削除 d を R への削除 T(d)=delete {t_1’(k_1’), t_2’(k_2’), _…, t_q’(k_q’)} from R; 変換する．このとき，δ(R∸{t_1’(k_1’), t_2’(k_2’), _…, t_q’(k_q’)})=δ(R) ∸{t_1’, t_2’, _…, t_q’}=δ(R)∸σ_φ(δ(R)) である．これはすべてのバッグ R と任意の削除 d に対して成立するので，「重複行削除ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

【2】重複行削除ビューは挿入不可能

 挿入不可能な重複行削除ビューの例を示す．たとえば，バッグ R={(1)(3)} の重複行除去ビュー δ(R)={(1)} に対して，挿入 i=insert {(2)} into δ(R) が発行されたとする．すると，i の R への変換は次のように無数に存在し一意ではない．したがって，「重複行削除ビューは挿入不可能である」という命題がスキーマレベルで成立する．
T_k(i)=insert {(2)(k)} into R; ここに k=1, 2, 3, _…

したがって，「重複行削除ビューは書換不可能である」という命題がスキーマレベルで成立する．

【3】加法和（⨄）ビューは削除可能

 加法和ビューを V=R⨄S とし，削除 d=deleteσ_φ(V) from V; が発行されたとき，削除の定義から次が成り立つ．
V∸σ_φ(V)= (R⨄S)∸σ_φ(R⨄S)=σ_¬φ(R⨄S)=σ_¬φ(R)⨄σ_¬φ(S) = (R∸σ_φ(R)) ⨄ (S∸σ_φ(S))．
したがって，削除 d= deleteσ_φ(V) from V; を実現するための必要かつ十分条件は d を T(d)に変換することである．
T(d)=begin; deleteσ_φ(R) from R; deleteσ_φ(S) from S; end;
このことはすべてのバッグ R, S, φ と任意の削除 d に対して成立するので，「加法和ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

なお，σ_φ(R⨄S)=σ_φ(R) ⨄σ_φ(S) の証明は次の通りである．
【命題１】σ_φ(R⨄S)=σ_φ(R) ⨄σ_φ(S) が成立する．
（証明）t(k)∈σ_φ(R⨄S) とすると，∃t(k_i)∈R∧∃t(ℓ_j)∈S∧k=k_i＋ℓ_j∧φ(t) が成り立つ．φ(t)=φ(t)∧φ(t) なので，(∃t(k_i)∈R∧φ(t))∧(∃t(ℓ_j)∈S∧φ(t))∧k= k_i＋ℓ_j が成り立つ．すなわち，∃t(k_i)∈σ_φ(R)∧∃t(ℓ_j)∈σ_φ(S)∧k= k_i＋ℓ_j が成り立つ．したがって，⨄ の定義により，
t(k)∈σ_φ(R) ⨄σ_φ(S) が成り立つ．逆に t(k)∈σ_φ(R) ⨄σ_φ(S) とすると，上記の逆の推論をたどることで t(k)∈σ_φ(R⨄S) であることを示せる．

Q.E.D.

【4】加法和（⨄）ビューは挿入不可能

 加法和ビューとそれに対して発行された挿入が変換不可能な一例を示す．
たとえば，和両立なバッグ R と S を R={(1)(3)}, S={(1)(2)} とするとき，加法和ビュー V=R⨄SはV={(1)(5)} である．このとき，V に対して挿入 i=insert {(2)(1)} into V; が発行されたとする．すると，i の変換は次の 2 通り考えられる．
T₁(i)=insert {(2)(1)} into R;
T₂(i)=insert {(2)(1)} into S;
このように変換に一意性がないので，「加法和ビューは挿入不可能である」という命題がスキーマレベルで成立する．

したがって，「加法和（⨄）ビューは書換不可能である」という命題がスキーマレベルで成立する．

【5】モーナス（∸）ビューは挿入不可能

 モーナスビューとそれに対して発行された挿入が変換不可能な一例を示す．
和両立なバッグ R と S を，たとえば R={(1)(3)}, S={(1)(2)} とするとき，モーナスビュー V=R∸S は V={(1)(1)} である．このとき，V に対して挿入 i=insert {(1)(2)} into V; が発行されたとする．すると，i の変換は次のように無数にあり一意ではない．
T_k(i)=begin; insert {(1)(2+k)} into R; insert {(1)(k)} into S; end; ここに k=0, 1, 2, 3, _…
したがって，i は変換可能ではない．このように反例を示せるので，「モーナスビューは挿入不可能である」という命題がスキーマレベルで成立する．

したがって，「モーナスビューは書換不可能である」という命題がスキーマレベルで成立する．

【6】バッグ共通ビューは挿入不可能

 バッグ共通ビューとそれに対して発行された挿入が変換不可能な一例を示す．
和両立なバッグ R と S を，たとえば R={(1)(3)}, S={(1)(2)} とするとき，V=R∩S={(1)(2)} である．このとき，V に対して挿入 i=insert {(1)(1)} into V; が発行されたとすると，i の変換は次の 2 通り考えられる．
T₁(i)=insert {(1)(1)} into S;
T₂(i)=begin; insert {(1)(1)} into R; insert {(1)(1)} into S; end;
つまり，変換は一意ではなく i は変換可能ではない．このように反例を示せるので，「バッグ共通ビューは挿入不可能である」という命題がスキーマレベルで成立する．

したがって，「バッグ共通ビューは書換不可能である」という命題がスキーマレベルで成立する．

【7】バッグ射影ビューは削除可能

 バッグ R の属性集合 X 上のバッグ射影ビューを V=π_X(R) とし，V へ削除 d= deleteσ_φ(V) from V; が発行されたとする．このとき σ_φ(V)=σ_φ(π_X(R)) である．
ところで，σ_φ(π_X(R))= π_X(σ_φ(R)) が成立する．
d: V←V∸σ_φ(V) であるから，V=V∸σ_φ(V)= π_X(R)∸π_X(σ_φ(R))= π_X(R∸σ_φ(R)) が成立する．したがって，d を実現するための必要かつ十分条件はそれを T(d) に変換することである．
T(d)=deleteσ_φ(R) from R;
このことはすべてのバッグ R, S, φ と任意の削除 d に対して成立するので，「バッグ射影ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

バッグ射影ビューとそれに対して発行された削除が変換可能な一例を示す．
【例題７】
バッグ　R(A, B)={(1, 1), (1, 2), (1, 3), (2, 1), (2, 2)}　とし，V=π_{A}(R)={(1)(3), (2)(2)} を R の {A} 上のバッグ射影ビューとする．このとき，V へ削除 d=delete σ_φ(V) from V; ここに φ=(A=1)，が発行されたとするとき，一意で副作用がなく余分な更新をしない d の変換は次の通りである．
T(d)=delete σ_A=1(R) from R;

【8】バッグ射影ビューは潜在キー保存ならば挿入可能

 バッグ R の属性集合 X 上のバッグ射影ビューを V=π_X(R) とするとき，バッグ射影ビュー V が潜在キー保存（concealed key preservation）であるとは，X がバッグ R の潜在主キー K を含むときをいう．
バッグ R の属性集合 X 上のバッグ射影ビューを V=π_X(R) とする．V への挿入 i=insert W into V; が発行されたとする．ここに W={w₁(k₁), w₂(k₂), _…, w_m(k_m)}，∀i((w_i, k_i)∈dom(V)) とする．
このとき，W からバッグ W～ を次のように生成する．ここに null は空を表す．
W～={w~₁(k₁), w~₂(k₂), _…, w~_m(k_m)}，ここに w~_i[X]=w_i かつ w~_i[ Ω_R－X]=(null, null, _…, null) とする．
このとき，V が潜在キー保存であるとすると，X は R の潜在主キー K を含み，潜在主キー属性が null をとることはないから，W と W～ の間には w(k)↔w~(k) という 1 対 1 の関係性が成立する．
また，π_X(R⨄W～)=π_X(R) ⨄π_X(W～)=π_X(R) ⨄W=V⨄W が成立するので，i を実現するための必要かつ十分条件は i を T(i)に変換することであることが分かる．
T(i)=insert W～ into R;
これは全てのバッグ射影ビュー V と挿入 i に対して成立するので，「バッグ射影ビューは潜在キー保存であれば挿入可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「バッグ射影ビューは潜在キー保存ならば書換可能である」という命題がスキーマレベルで成立する．

なお，「潜在キー保存」という条件自体はスキーマレベルの検証であるが，この検証を通過しただけでは「潜在キー制約」に抵触してしまう可能性がある．そのためにはインスタンスレベルの検証が必須となることは，3.2 節【10】項「射影ビューはキー保存ならば更新可能」のところで指摘したことと同様である．

【9】バッグ選択ビューは削除可能

 バッグ R のバッグ選択ビューを V=σ_φ (R) とし，V への削除 d=deleteσ_ψ(V) from V; が発行されたとする．ここに ψ は探索条件である．X=σ_ψ(V) とすると，V=σ_φ (R) なので，X=σ_ψ(V)=σ_ψ(σ_φ (R))=σ_ψ∧φ (R)となる．
そこで，d を次に示す T(d) に変換する．
T(d)=deleteσ_ψ∧φ(R) from R;
このとき，
σ_φ(R∸σ_ψ∧φ(R))=σ_φ(R)∸σ_φ(σ_ψ∧φ(R)))=σ_φ(R)∸σ_ψ∧φ(R)=σ_φ(R)∸σ_ψ(σ_φ(R))=V∸σ_ψ(V) が成立する．
この性質は全てのバッグ選択ビュー V と削除 d に対して成立するので，「バッグ選択ビューは削除可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

【10】バッグ選択ビューは挿入可能

 バッグ R のバッグ選択ビューを V=σ_φ (R) とし，V への挿入 i=insert X into V; ここに X⊆dom(V) が発行されたとする．dom(V)= dom(σ_φ(R))=σ_φ(dom(R)) なので，X⊆σ_φ(dom(R)) である．このとき，σ_φ(σ_φ(dom(R)))=σ_φ(dom(R)) なので，σ_φ (X)=X である．
そこで，i を T(i) に変換する．
T(i)=insert X into R;
このとき，σ_φ (R ⨄X)=σ_φ (R) ⨄σ_φ (X)=V ⨄X が成立する．
この性質は全てのバッグ選択ビュー V と挿入 i に対して成立するので，「バッグ選択ビューは挿入可能である」という命題がスキーマレベルで成立する．なお，T が定義 1 の条件 (a)～(c) を満たしていることはその定義から明らかである．

したがって，「バッグ選択ビューは書換可能である」という命題がスキーマレベルで成立する．

【11】バッグ θ-結合ビューは削除・挿入・書換不可能

 バッグ θ-結合ビューの更新可能性については，リレーショナル代数での θ-結合ビューの更新可能性がスキーマレベルで削除，挿入，いずれも不可能なので，バッグビューのそれについても不可能となる．

4.4 一般的バッグビューの更新可能性（スキーマレベル）

 表 5「基本的バッグビューの更新可能性（スキーマレベル）」は 4.3 節の議論の結果をまとめたものです．一般的バッグビューの更新可能性の判定は，3.3 節で論じた一般的リレーショナルビューの更新判定と全く同じように，作成した一般的バッグビューの定義木をトップダウンに，たとえば幅優先探索で走査しながら，ノードごとでその更新可能性を表 5 に参照していけば，その更新可能性をスキーマレベルで検証することができます．

5．おわりに

 本稿ではリレーショナルビューとバッグビューの更新可能性をスキーマレベルで論じその全貌を明らかにしました．集合であればバッグですが，逆は成立しないので，当然のこととして，リレーショナルビューが更新可能であっても，それを潜在リレーションとするバッグビューが更新可能となる保証はありません．その違いは表 3 と表 5 を比較することで一目瞭然かと思います．
末筆ながら，理論と実践のはざまに言及しておくと次のとおりです．SQL はバッグ意味論に基づいたリレーショナルデータベース言語なので，SQL でのビューの更新可能性は本稿の表 5 に示したバッグビューの更新可能性に基づき規格化されてしかるべきす．しかしながら，現実には SQL が理論に先行してしまいました．それには歴史的理由があって，バッグビューの更新可能性の理論的研究は 1990 年代に入ってから盛んになったのですが，ビューとその更新可能性の重要性をいち早く認識していた SQL はその初めての国際標準規格である SQL-87 を制定した 1987 年時点でその規格化の第一歩を踏み出していました．そこでの原則は極めて現実的で，SQL-87 を改正した SQL-92 に見るように「更新が可能なビューは，実表から選択または射影だけを行っており，ビュー表の行および列が基となる実表の行および列と 1 対 1 に対応している場合である」というものでした．SQL-87 は SQL-92, SQL:1999, SQL:2003, SQL:2008, SQL:2011 等を経て最新規格の SQL:2016 まで改正され続け，少しでも多様なビューを更新可能にしようとビューとその更新可能性の規格も改正され続けてきましたが，「1 対 1 の対応」という基本的考え方に変更はないようです．本稿で論じたように，バッグビューの更新可能性はあくまで理論的であってそのような呪縛とは無縁です．SQL:2023 が近々発表されるようですが，何か変化はあるのでしょうか，注目したいと思います．
なお，本稿ではビューの更新可能性をスキーマレベルで論じましたが，その対極にある「インスタンスレベルアプローチ」や「SQL のビューサポート」については機会を得て報告できればと思います．

【文献】

[1]

Edgar F. Codd. A Relational Model of Data for Large Shared Data Banks. Communications of the ACM, Vol.13, No.6, pp.377-387, 1970.

[2]

Edgar F. Codd. Recent Investigations in Relational Database Systems. Information Processing 74, pp. 1017-1021, North-Holland, 1974.

[3]

Michael Stonebraker, Eugene Wong, Peter Kreps, and Gerald Held. The Design and Implementation of INGRES. ACM Transactions on Database Systems, Vol. 1, No. 3, pp. 189-222, September 1976.

[4]

Umeshwar Dayal and Philip A. Bernstein. On the Updatability of Relational Views. Proceeding of VLDB 1978, pp.368-377, 1978.

[5]

Edgar F. Codd. Extending the Database Relational Model to Capture More Meaning. ACM TODS, Vol.4, No.4, pp.397-434, 1979.

[6]

増永 良文，長田 悠吾，石井 達夫. 更新意図の外形的推測に基づいたビューの更新可能性とその PostgreSQL 上での実現可能性検証. 日本データベース学会和文論文誌 Vol.18-J, Article No.1, 2020 年 3 月．

[7]

増永 良文，長田 悠吾，石井 達夫. 整合ラベリング問題としてのクロス結合ビューの更新可能性. 日本データベース学会和文論文誌 Vol.19-J, Article No.1, 2021 年 3 月．

[8]

Joseph Albert. Algebraic Properties of Bag Data Types. Proceedings of the 17th International Conference on Very Large Databases, pp.211-219, 1991．

[9]

Wayne D. Blizard. Multiset Thoery. Notre Dame Journal of Formal Logic, Vol.30, No.1. pp.36-66, Winter 1989.

[10]

増永良文．リレーショナルデータベース入門[第3版]，サイエンス社，2017．