1. はじめに
リレーショナルデータベース(RDB)を設計するにあたり,「リレーションは第 3 正規形(3NF)にしましょう」とはよく言われることです.リレーションの正規化理論によると,3NF への分解が情報無損失であることは間違いのないことですが,その際,関数従属性は保存されるのか,されないのか?このことについて,どうも不確かな認識が流布しているのではないか?と思われる事例に遭遇したので,この記事を書く気になりました.
その事例とは,何気なく過去の「データベーススペシャリスト試験問題」を眺めていた時に目に留まった次の設問と解答です.
問 4
| 関係モデルにおいて,情報無損失分解ができ,かつ,関数従属性保存が成り立つ変換が必ず存在するものはどれか。ここで,情報無損失分解とは自然結合によって元の関係が必ず得られる分解をいう。 |
ア 第 2 正規形から第 3 正規形への変換
イ 第 3 正規形からボイスコッド正規形への変換
ウ 非正規形から第 1 正規形への変換
エ ボイスコッド正規形から第 4 正規形への変換
この問題の正解は「ア」とされています[2].
さて,この設問と正解を眺めていて釈然としない点が 2 つありました.
一つは,情報無損失分解の定義は与えられていますが,「関数従属性保存」の定義が与えられていません.果たして,どういう意味でこの用語を使っているのでしょうか?
もう一つは,「情報無損失分解ができ,かつ,関数従属性保存が成り立つ変換が必ず存在するもの」を問うていますが,「必ず」とは一体どのような意味で使っているのでしょうか?「ア」を正解とするということなので,「リレーションの第 2 正規形から第 3 正規形への変換は必ず情報無損失分解かつ関数従属性保存である」が出題者の意図ではないかと推察されますが,本当にそうなのでしょうか?
そこで,本稿では,この問題を少しばかり深堀してみることとしました.
2. 基礎的事項
議論を進めるために必要な概念を整理しておきます.
【定義 1】(リレーションスキーマとリレーション)
リレーションスキーマ R とはリレーション名 R と属性のリスト A1, A2, …, An からなり,R(A1, A2, …, An) と表される.dom をドメイン関数とするとき,R⊆dom(A1)×dom(A2)×…×dom(An) をリレーションスキーマ R のインスタンス,あるいは dom(A1),dom(A2),…,dom(An) 上のリレーション R という.
リレーションスキーマ R である性質 P が成立するとは R のすべてのインスタンス R で P が成立するときおよびその時のみをいう.
【定義 2】(関数従属性)
リレーションスキーマ R で関数従属性(functional dependency, FD) f=X→Yが成立するとは,次が成立するときをいう.ここに,R∈R は R が R のインスタンスであることを表す.
(∀R∈R)(∀t, t’∈R)(t[X]=t‘[X]⇒t[Y]=t‘[Y])
【定義 3】(所与の関数従属性集合)
リレーションスキーマ R に所与の(given)関数従属性の集合 F={f1, f2, …, fp},ここに(∀i= 1, 2, …, p)(fi=Xi→Yi ∧ Xi, Yi⊆ΩR),を指定できる.ここで,ΩR は R の全属性集合 {A1, A2, …, An} を表し,一般に X, Y を集合とするとき,X⊆Y は X が Y の部分集合であることを,X⊂Y は X が Y の真部分集合(proper subset)であることを表す.
【定義 4】(関数従属性集合の閉包)
リレーションスキーマ R に所与の関数従属性の集合 F が指定されているとする.このとき, F の閉包 F+ は次のように定義される.ここに,F ⊨ X→Y は X→Y がアームストロングの公理系のもとで F から導出されることを表す.
F+={X→Y | X, Y⊆ΩR ∧ F ⊨ X→Y}
つまり,F+ は F が与えられたとき, F を基にして R 上で成立するすべての FD からなる集合を表します.F+ を求めるアルゴリズムを示しますが,その前に,次が成立することに注目します.ここに, X+ は F に関する X の閉包を表し,iff は if and only if,すなわち必要かつ十分条件を表します.
(∀X, Y⊆ΩR)(X→Y∈F+ iff Y⊆X+)
なお,X+ を求めるアルゴリズムは次のとおりです.このアルゴリズムの時間計算量は多項式時間であり,扱いやすい(tractable)問題です.
【X+ を求めるアルゴリズム】
1. X(0)=Xとおく.
2. X(i)= X(i-1)∪{A|A∈Z ∧ Y→Z∈F ∧ Y⊆X(i-1)} (i≧1)とする.
3. もし,X(i)= X(i-1) ならX+= X(i-1) とおく.そうでなければステップ 2 にいく.
【例題1】
リレーションスキーマ R(A, B, C) に所与の FD 集合 F={A→B, B→C}が指定されているとする.たとえば,X={A} としてX+ を求めると,ステップ 1 で X(0)={A}, ステップ 2 と 3 を繰り返して,X(1)= X(0)∪{B}, X(2)= X(1)∪{C} (={A, B, C}), X(3)= X(2) となり, X+={A, B, C}を得る.
さて,F+ を求めるアルゴリズムは次のとおりです.
【F+ を求めるアルゴリズム】
1. F+=Φ とおく.
2. 2ΩR-Φ の各元 X に対してその閉包 X+を求め,F+ = F+∪{X→X+} とする.
3. ステップ 2 の操作が全て終了すれば,その時の F+ が求める結果である.
ステップ 2 で,2ΩR-Φ の各元 X に対してその閉包 X+ を求めていることから明らかなように,このアルゴリズムの時間計算量は O(2|ΩR|),ここに O はオーダー関数,|ΩR |は ΩR の濃度を表す,と指数時間となり,扱いにくい(intractable)問題であることが分かります.つまり,上記のアルゴリズムは|ΩR |が小さいときは問題なく動きますが,それが大きくなるにつれてとんでもない時間を要することになります.
なお,リレーションの情報無損失分解に係る関数従属性保存を論じるためには,F+ の属性集合Z(⊆ΩR)上の射影 F+[Z] を定義する必要がありますが(定義 5),それを端的に行うためにはステップ 3 をステップ 3’ に置き換えておくと都合がよいのでそのようにします(射影と関わらない議論はステップ 3 で得られた F+ を念頭に置いて行っています).
3’. ステップ 2 の操作が全て終了すれば,その時の F+ が求める結果であるが,もし
F+ の元 X→X+ の被決定子が X+=A1A2…Aq(Ai∈ΩR, q≧2)のように単一の属性で
でなければ,X→X+ をX→A1, X→A2, …, X→Aq置き換えた F+ を求める結果とする
(この置換えは,X→YZ iff X→Y ∧ X→Z が成立することによる).
ここに,一般に A1A2…Aq は集合{A1, A2, … , Aq} の簡略表現とする(以下,同様).
したがって,たとえば AB={A, B}={B, A}=BA である.
【例題2】
リレーションスキーマ R(A, B, C)に所与の FD 集合 F={A→B, B→C} が指定されているとする.このとき,F+ を求めると,2ΩR={Φ, A, B, C, AB, AC, BC, ABC} であるので,ステップ 1 で F+=Φ,ステップ 2 と 3 を繰り返して,A+=ABC, B+=BC, C+=C, AB+=ABC, AC+=ABC, BC+=BC, ABC+=ABC なので,ステップ 3 で F+ は次のようになる.
F+={A→ABC, B→BC, C→C, AB→ABC, AC→ABC, BC→BC, ABC→ABC}
F+をステップ 3 ではなくステップ 3’ を用いて求めた場合,それは次のようになる.
F+={A→A, A→B, A→C, B→B, B→C, C→C, AB→A, AB→B, AB→C, AC→A,
AC→B, AC→C, BC→B, BC→C, ABC→A, ABC→B, ABC→C}
なお,一般に F+ には A→A や AB→A など自明な FD も含まれているが,F+ はそれらも含めて R 上で成り立つ関数従属性の全てからなる集合を表しているということである.
【定義5】(関数従属性集合の閉包の射影)
リレーションスキーマ R に所与の関数従属性の集合 F が指定されているとする.このとき,一般に Z⊆ΩR として,F+ の Z 上の射影 F+[Z]は次のように定義される.ここに F+ はステップ 3’ を用いて求められており,A∈ΩR である.
F+[Z]={X→A|X→A∈F+ ∧ X∪A⊆Z}
【例題3】
リレーションスキーマ R(A, B, C)に所与の FD 集合 F={A→B, B→C} が指定されているとする.このとき,F+ の {B, C} 上の射影,F+[B, C] は次のようになる.
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C }
なお,B, C∈ΩR としたとき,F+[B, C]は本来は F+[{B, C}]あるいは F+[BC]と書くべきであるが,慣習的に F+[B, C]と書くことも多く,本稿でもそれに倣っている.
【定義6】(リレーションスキーマの情報無損失分解)
リレーションスキーマ R の情報無損失分解は F+ の元 X→Y (X,Y⊆ΩR)を使って R を 2 つの射影 R[X∪Y]と R[ΩR-Y],ここに - は差集合演算を表す,に分解することをいう.
FD による分解はリレーションスキーマが 2 つの射影に情報無損失分解されるための十分条件なので,この分解は情報無損失,すなわち R=R[X∪Y]*R[ΩR-Y]が成立することは改めて言うまでもないことです.ここに * は自然結合演算を表しています.
ここで,念のためにリレーションスキーマが第 2 正規形(2NF),第 3 正規形(3NF)そしてボイス‐コッド正規形(BCNF)であることの定義を確認しておきます.「リレーションスキーマ R が第 2 正規形(2NF)であるとは,R は 1NF であって,R の全ての非キー属性は R の各候補キーに完全関数従属している」こと,「リレーションスキーマ R が第 3 正規形(3NF)であるとは,R は 2NF であって,R の全ての非キー属性は R のいかなる候補キーにも推移的に関数従属しない」こと,そして,リレーションスキーマ R がボイス‐コッド正規形(BCNF)であるとは,「X→Yを R の関数従属性とするとき,X→Y は自明な FD であるか,あるいは X は R のスーパーキーである」ことです.
なお,リレーショナルデータモデルと正規化理論の原典に立ち戻って RDB 設計の分解的手法を今一度整理しておきたい向きには文献[3, 4]を,本稿では立ち入らないが分解的手法と対極をなす RDB 設計の合成的手法の原典にあたりたい向きには文献[5]を,そしてそれらをカバーした書籍として拙著[6]を薦めます.
3. 関数従属性保存とは
まず,リレーションスキーマの情報無損失分解に係る関数従属性保存の定義を与えます.
【定義7】(関数従属性保存)
リレーションスキーマ R に所与の関数従属性の集合 F が指定されているとする.X→Y∈F+ として,X→Y による R の R[X∪Y] と R[ΩR-Y]への情報無損失分解が関数従属性保存とは,次が成立するときをいう.
(F+[X∪Y]∪F+[ΩR-Y])+=F+
つまり,F の閉包 F+ の X∪Y 上の射影 F+[X∪Y] とその ΩR-Y 上の射影 F+[ΩR-Y]の和集合の閉包 (F+[X∪Y]∪F+[ΩR-Y])+ が F+ と等しいかどうかを問うていて,両者が等しいときに,関数従属性保存と言います.決して F[X∪Y]∪F[ΩR-Y]=F を問うているわけではないことに注意してください.あくまで,閉包レベルの概念です.
なお,一般にリレーションスキーマ R を X→Y でR[X∪Y]と R[ΩR-Y]へ情報無損失分解したとき,もし R[ΩR-Y]に Z→W∈F+(ここに,Z∪W⊂ΩR-Y)が存在していると,R[ΩR-Y]は R[Z∪W]と R[ΩR-Y-W]へ情報無損失分解可能で,結果として R は R[X∪Y]と R[Z∪W]と R[ΩR-Y-W]に情報無損失分解できます.このとき,上記の関数従属性保存の定義は素直に次のように拡張されます(この拡張はより一般的な形で可能です).
(F+[X∪Y]∪F+[Z∪W]∪F+[ΩR-Y-W])+=F+
以上で準備は整いました.ここからは 2NF ではあるが 3NF ではないリレーションスキーマの 3NF への情報無損失分解が関数従属性保存か否かを検証していきます.3 つのパターンが示されますが,それらの結果は大変興味深いものです.
4. 3NF 分解が関数従属性保存である例
【例題4】
リレーションスキーマ R(A, B, C) に所与の FD 集合 F={A→B, B→C} が指定されているとする.このとき,R は 2NF ではあるが 3NF ではない.R の 3NF への情報無損失分解が関数従属性保存であるかどうかを検証してみよ.なお,図 1 に本例題での所与の FD 集合の様子を示す.
(解答)
例題 2 で示したように,F+={A→A, A→B, A→C, B→B, B→C, C→C, AB→A, AB→B, AB→C, AC→A, AC→B, AC→C, BC→B, BC→C, ABC→A, ABC→B, ABC→C} である.
まず,確認すれば R は 2NF ではあるが 3NF ではない.なぜならば,推移的関数従属性 A→B→C が存在するからである.そこで,A→B→C の解消を図るため,B→C を用いて,R を R[B, C]と R[A, B] に情報無損失分解する.このとき,F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C},F+[A, B]= {A→A, A→B, B→B, AB→A, AB→B}となる.
さて,G=F+[B, C]∪F+[A, B]と置いて,F+と G の元を見比べてみると,F+ の元 A→C,AB→C, AC→A,AC→B,AC→C,ABC→A,ABC→B,ABC→C が G に入っていない.そこで,これらの元で自明でないA→C,AB→C, AC→B について,それらが G+ の元であるかどうかを検証する.
まず,A→C は,(A→B∈F+[A, B])∧(B→C∈F+[B, C])なので,アームストロングの公理系の推移律から A→C∈G+ であることが分かる(つまり,G ⊨ A→C である).AB→C は,(AB→B∈F+[A, B]) ∧(B→C∈F+[B, C])なので,アームストロングの公理系の推移律から AB→C∈G+ であることが分かる(G ⊨ AB→C).AC→B については,A→B∈F+[A, B]なので,アームストロングの公理系の添加律から AC→BC で,BC→B∈F+[B, C] なので,アームストロングの公理系の推移律から AC→B∈G+ であることが分かる(G ⊨ AC→B).したがって,G+=F+ となり,この情報無損失分解は関数従属性保存である.
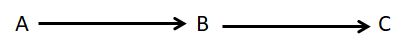
前述の平成 26 年度 春季 データベーススペシャリスト試験 午前Ⅱ 問題 問 4 が(ア)を正解としたのは,例題 4 のような状況を想定しての設問だったのかもしれませんが,そのような但し書きは一切ありません,しかしながら,3NF 分解と関数従属性保存の関係性は常にこのように単純というわけではなく,以下に見るように,その出題意図に反した例を多々示すことができます.
5. いかなる 3NF 分解も関数従属性保存でない例
【例題5】
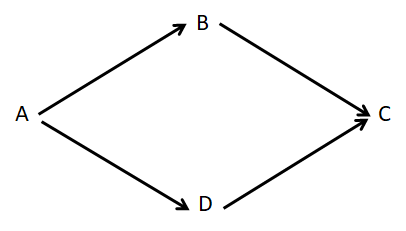
リレーションスキーマ R(A, B, C, D) に所与の FD 集合 F={A→B, B→C, A→D, D→C} が指定されているとする.このとき,R は 2NF ではあるが 3NF ではない.R の 3NF への情報無損失分解が関数従属性保存であるかどうかを検証してみよ.なお,図 2 に本例題での所与の FD 集合の様子を示す.
(解答)
このとき,A+=ABCD, B+=BC, C+=C, D+=CD, AB+=AC+=AD+=ABCD, BC+=BC, BD+=BCD, CD+=CD, ABC+=ABD+=ACD+=ABCD, BCD+=BCD, ABCD+=ABCD なので,F+={A→A, A→B, A→C, A→D, B→B, B→C, C→C, D→C, D→D, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→B, BC→C, BD→B, BD→C, BD→D, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D}となる.R の候補キーはAのみなので 2NF である.一方,R にはA→B→C,A→D→Cという 2 つの推移的関数従属性が存在し 3NF ではないので R を情報無損失分解する.
(場合1) A→B→C の解消を図る.
R を A→B→C を構成する B→C を使って R[B, C] と R[A, B, D]に情報無損失分解すると,次が成立する.このときは R[A, B, D] も 3NF となっている.
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C}
F+[A, B, D]= {A→A, A→B, A→D, B→B, D→D, AB→A, AB→B, AB→D, AD→A, AD→B, AD→D, BD→B, BD→D, ABD→A, ABD→B, ABD→D}
そこで,G=F+[B, C]∪F+[A, B, D] と置き,G+=F+ かどうかを検証する.F+ と G の元を見比べてみると, F+ の元 A→C, D→C, AB→C, AC→A, AC→B, AC→C, AC→D, AD→C, BD→C, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→C, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D が G に入っていない.これらの中の自明でない FD である A→C, D→C, AB→C, AC→B, AC→D, AD→C, BD→C, ABC→D, ACD→B が G+ の元か否かを検証すると,D→C が G の下では導出されないことが分かる(¬(G ⊨ D→C),ここに¬は否定を表す).したがって,この情報無損失分解は関数従属性保存ではない.
(場合2) A→D→C の解消を図る.
R を A→D→C を構成する D→C を使って R[D, C] と R[A, B, D] に情報無損失分解したときには,(場合1)と同様な展開で B→C が保存されず,この情報無損失分解も関数従属性保存ではないない.
つまり,リレーションスキーマ R(A, B, C, D) に所与の FD 集合 F={A→B, B→C, A→D, D→C} が指定されているとき,R を 3NF に正規化しようとする何れの情報無損失分解も関数従属性保存ではないことが示されました.これが,前述の午前 Ⅱ 問題 問 4 とその正解を(ア)とする解答への端的な反証となります.
6. 3NF 分解が関数従属性保存となるか否かが,場合による 3 例
【例題6】
リレーションスキーマ R(A, B, C, D)に所与の FD 集合 F={A→B, B→C, C→D} が指定されているとする.このとき,R は 2NF ではあるが 3NF ではない.R の 3NF への情報無損失分解が関数従属性保存であるかどうかを検証してみよ.なお,図 3 に本例題での所与の FD 集合の様子を示す.
(解答)
このとき,F+={A→A, A→B, A→C, A→D, B→B, B→C, B→D, C→C, C→D, D→D, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→B, BC→C, BC→D, BD→B, BD→C, BD→D, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D}
R の候補キーは A のみなので 2NF である.一方,R には A→B→C,A→B→D,B→C→D,A→C→D という 4 つの推移的関数従属性が存在し 3NF ではないので R を情報無損失分解する.
(場合1) A→B→C の解消を図る.
R を A→B→C を構成する B→C を使って R[B, C] と R[A, B, D] に情報無損失分解すると,A→B→D により,R[A, B, D] も 3NF ではないので,それを B→D を使って R[B, D] と R[A, B]に情報無損失分解すると次が成立する.
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C}
F+[B, D]= {B→B, B→D, D→D, BD→B, BD→D}
F+[A, B]= {A→A, A→B, B→B, AB→A, AB→B}
そこで,G=F+[B, C]∪F+[B, D]∪F+[A, B] と置き,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→C, A→D, C→D, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A,AD→B, AD→C, AD→D, BC→D, BD→C, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→Dである.これらのうち,自明でない FD である A→C, A→D, AB→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D, BD→C, ABC→D, ABD→C, ACD→B, BCD→A について,それらが G+ の元か否かを検証すると,C→D が F+ の元ではないことが分かる(¬(G ⊨ C→D)).したがって,この情報無損失分解は関数従属性保存ではない.
(場合2) A→B→D の解消を図る.
R を A→B→D を構成する B→D を使って R[B, D] と R[A, B, C] に情報無損失分解すると,A→B→C により,R[A, B, C] も 3NF ではないので,それを B→C を使って R[B, C] と R[A, B] に情報無損失分解すると次が成立する.その結果,R は R[B, D] と R[B, C] と R[A, B] に情報無損失分解されるが,検証しないといけないことは (場合1)と同様となる.したがって,この情報無損失分解は関数従属性保存ではない.
(場合3) B→C→D の解消を図る.
R を B→C→D を構成する C→D を使って R[C, D] と R[A, B, C] に情報無損失分解すると,A→B→C により,R[A, B, C] も 3NF ではないので,それを B→C を使って R[B, C] と R[A, B]に情報無損失分解すると次が成立する.
F+[C, D]= {C→C, C→D, D→D, CD→C, CD→D}
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C}
F+[A, B]= {A→A, A→B, B→B, AB→A, AB→B}
そこで,G=F+[C, D]∪F+[B, C]∪F+[A, B] と置き,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→C, A→D, B→D, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→D, BD→B, BD→C, BD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D である.これらのうち,自明でない FD である A→C, A→D, B→D, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D, BD→C, ABC→D, ABD→C, ACD→B について,それらが G+ の元か否かを検証すると,すべてが G+ の元であることが分かる.したがって,この情報無損失分解は関数従属性保存である.
(場合4) A→C→D の解消を図る.
R を A→C→D を構成する C→D を使って R[C, D] と R[A, B, C]に情報無損失分解する.このとき,行わなくてはならない検証は(場合3)と同じとなり,したがって,この情報無損失分解は関数従属性保存である.
以上,例題 6 では,関数従属性保存か否かは情報無損失分解の仕方による,ということが示されました.
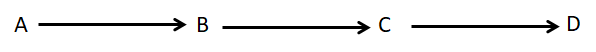
【例題7】
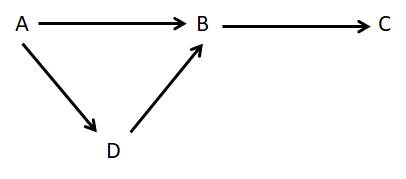
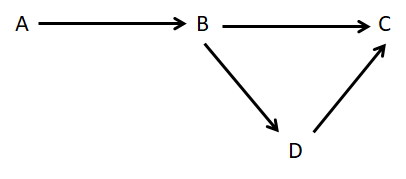
リレーションスキーマ R(A, B, C, D) に所与の FD 集合 F={A→B, B→C, A→D, D→B} が指定されているとする.このとき,R は 2NF ではあるが 3NF ではない.R の 3NF への情報無損失分解が関数従属性保存であるかどうかを検証してみよ.なお,図 4 に本例題での所与の FD 集合の様子を示す.
(解答)
このとき,A+=ABCD, B+=BC, C+=C, D+=BCD, AB+=AC+=AD+=ABCD, BC+=BC, BD+=BCD, CD+=BCD, ABC+=ABD+=ACD+=ABCD, BCD+=BCD, ABCD+=ABCD なので,F+ は次の通りとなる.
F+={A→A, A→B, A→C, A→D, B→B, B→C, C→C, D→B, D→C, D→D, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→B, BC→C, BD→B, BD→C, BD→D, CD→B, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D}
R の候補キーは A のみで,2NF である.一方,R には A→B→C, A→D→B, D→B→C, A→D→C という 4 つの推移的関数従属性が存在し 3NF ではない.そこで,R を 3NF に情報無損失分解する.
(場合1) A→B→C の解消を図る.
R を A→B→C を構成する B→C を使って R[B, C] と R[A, B, D] に情報無損失分解すると,A→D, D→B∈F+ なので,R[A, B, D] は 3NF ではなく,それを D→B で情報無損失分解して 3NF にするとき,次が成立する.
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C}
F+[A, D]= {A→A, A→D, D→D, AD→A, AD→D}
F+[B, D]= {B→B, D→B, D→D, BD→B, BD→D}
そこで,G=F+[B, C]∪F+[A, D]∪F+[B, D] と置き,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→B, A→C, D→C, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→B, AD→C, BD→C, CD→B, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D である.これらのうち,自明でない FD である A→B, A→C, D→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BD→C, CD→B, ABC→D, ABD→C, ACD→B について,それらが G+ の元か否かを検証すると,すべてが G+ の元であることが分かる.したがって,この情報無損失分解は関数従属性保存である.
(場合2) A→D→B の解消を図る.
R を A→D→B を構成する D→B を使って R[D, B] と R[A, C, D] に情報無損失分解すると,A→D, D→C∈F+ なので,R[A, C, D] は 3NF ではなく,それを D→C で情報無損失分解して 3NF にするとき,次が成立する.
F+[D, B]= {B→B, D→B, D→D, BD→B, BD→D}
F+[C, D]= {C→C, D→C, D→D, CD→C, CD→D}
F+[A, D]= {A→A, A→D, D→D, AD→A, AD→D}
そこで,G=F+[D, B]∪F+[C, D]∪F+[A, D] と置き,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→B, A→C, B→C, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→B, AD→C, BC→B, BC→C, BD→C, CD→B, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D となる.これらのうち,自明でない FD である A→B, A→C, B→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BD→C, CD→B, ABD→C, ACD→B について,G+ の元であるか否かを検証すると,B→C が G+ の元ではないことが分かる(¬(G ⊨ B→C)).したがって,この情報無損失分解は関数従属性保存ではない.
(場合3) D→B→C の解消を図る.
R を D→B→C を構成する B→C を使って情報無損失分解することとなるが,このとき,行わなくてはならない検証は(場合1)と同じとなり,したがって,この情報無損失分解は関数従属性保存である.
(場合4) A→D→C の解消を図る.
R を A→D→C を構成する D→C を使って R[D, C] と R[A, B, D] に情報無損失分解すると,A→D, D→B∈F+ かつ ¬(D→A∈F+) なので,R[A, B, D]は 3NF ではなく,それを D→B で情報無損失分解して 3NF にするとき,次が成立する.
F+[D, C]= {C→C, D→C, D→D, CD→C, CD→D}
F+[D, B]= {B→B, D→B, D→D, BD→B, BD→D}
F+[A, D]= {A→A, A→D, D→D, AD→A, AD→D}
そこで,G=F+[D, C]∪F+[D, B]∪F+[A, D] と置き,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→B, A→C, B→C, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→B, AD→C, BC→B, BC→C, BD→C, CD→B, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D となる.
これらのうち,自明でない FD である A→B, A→C, B→C, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→B, AD→C, BC→B, BC→C, BD→C, CD→B, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D について,G+ の元であるか否かを検証すると,B→C が G+ の元ではないことが分かる(¬(G ⊨ B→C)).したがって,この情報無損失分解は関数従属性保存ではない.
以上,例題 7 では,関数従属性保存か否かは情報無損失分解の仕方による,ということが示されました.
【例題8】
リレーションスキーマ R(A, B, C, D) に所与の FD 集合 F={A→B, B→C, B→D, D→C} が指定されているとする.このとき,R は 2NF ではあるが 3NF ではない.R の 3NF への情報無損失分解が関数従属性保存であるかどうかを検証してみよ.なお,図 5 に本例題での所与の FD 集合の様子を示す.
(解答)
このとき,A+=ABCD, B+=BCD, C+=C, D+=CD, AB+=AC+=AD+=ABCD, BC+=BCD, BD+=BCD, CD+=CD, ABC+=ABD+=ACD+=ABCD, BCD+=BCD, ABCD+=ABCD なので,F+ は次の通りとなる.
F+={A→A, A→B, A→C, A→D, B→B, B→C, B→D, C→C, D→C, D→D, AB→A, AB→B, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→B,BC→C, BC→D, BD→B, BD→C, BD→D, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D}
R の候補キーは A のみで,2NF である.一方,R には A→B→C,A→B→D, B→D→C,A→D→C という 4 つの推移的関数従属性が存在し 3NF ではない.そこで,R を情報無損失分解する.
(場合1) A→B→C の解消を図る.
この場合,B→C を使って R を R[B, C] と R[A, B, D] に情報無損失分解する.R[A, B, D] では A→B→D が成立していて 3NF ではないので,B→D でそれを R[B, D] と R[A, B] に情報無損失分解する.このとき,次が成立する.
F+[B, C]= {B→B, B→C, C→C, BC→B, BC→C }
F+[B, D]= {B→B, B→D, D→D, BD→B, BD→D}
F+[A, B]= {A→A, A→B, B→B, AB→A, AB→B}
そこで,G=F+[B, C]∪F+[B, D]∪F+[A, B] と置いて,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.
そのような元は,A→C, A→D, D→C, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→D, BD→C, CD→C, CD→D, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D となる.これらのうち,自明でない FD である A→C, A→D, D→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D, BD→C, ABC→D, ABD→C, ACD→B について,G+ の元であるか否かを検証すると,唯一,D→C が G の下では導出されない,つまり,D→C は G+ の元ではないことが分かる(¬(G ⊨ D→C)).したがって,この情報無損失分解は関数従属性保存ではない.
(場合2) A→B→D の解消を図る.
この場合,B→D を使って R を R[B, D] と R[A, B, C] に情報無損失分解する.R[A, B, C] は 3NF ではないので,B→C でそれを R[B, C] と R[A, B] に情報無損失分解する.このとき,行わなくてはならない検証は(場合1)と同じとなり,したがって,この情報無損失分解は関数従属性保存ではない.
(場合3) B→D→C の解消を図る.
この場合,D→C を使って R を R[D, C] と R[A, B, D] に情報無損失分解する.R[A, B, D] は A→B→D の存在により 3NF ではないので,B→D でそれを R[B, D] と R[A, B] に情報無損失分解する.このとき,次が成立する.
F+[C, D]= {C→C, D→C, D→D, CD→C, CD→D }
F+[B, D]= {B→B, B→D, D→D, BD→B, BD→D}
F+[A, B]= {A→A, A→B, B→B, AB→A, AB→B}
そこで,G=F+[C, D]∪F+[B, D]∪F+[A, B] と置いて,G+=F+ かどうかを検証する.そのために,F+ の元であって G の元でない FD について,それが G+ の元であるか否かを検証する.そのような元は,
A→C, A→D, B→C, AB→C, AB→D, AC→A, AC→B, AC→C, AC→D, AD→A, AD→B, AD→C, AD→D, BC→B, BC→C, BC→D, BD→C, ABC→A, ABC→B, ABC→C, ABC→D, ABD→A, ABD→B, ABD→C, ABD→D, ACD→A, ACD→B, ACD→C, ACD→D, BCD→B, BCD→C, BCD→D, ABCD→A, ABCD→B, ABCD→C, ABCD→D となる.これらのうち,自明でない FD である A→C, A→D, B→C, AB→C, AB→D, AC→B, AC→D, AD→B, AD→C, BC→D, BD→C, ABC→D, ABD→C, ACD→B について,G+ の元であるか否かを検証すると,すべてが G の下で導出されることが分かる.したがって,この情報無損失分解は関数従属性保存である.
(場合4) A→D→C の解消を図る.
この場合,D→C を使って R を R[D, C] と R[A, B, D] に情報無損失分解する.このとき,行わなくてはならない検証は(場合3)と同じとなり,したがって,この情報無損失分解は関数従属性保存である.
以上,例題 8 でも,関数従属性保存か否かは情報無損失分解の仕方による,ということが示されました.
以上,例題 4~8 を通して確認できたように,「情報無損失分解ができ,かつ,関数従属性保存が成り立つ変換が必ず存在するものは,第 2 正規形から第3正規形への変換である」(午前 Ⅱ 問題 問 4 の出題意図)とは言い切れないことが分かりました.関数従属性保存が成り立つか否かは場合によるということです.
7. おわりに
筆者は,平成 26 年度 春季 データベーススペシャリスト試験 午前 Ⅱ 問題 問 4 とその正解を「出題ミス」として簡単に片付けてしまう気にはなれず,この問題をもう少し重く受け止めています.その理由は,なぜこのような認識がなされてしまったのだろうかと考えるとき,どうもその背景には RDB 設計の現場に,RDB 設計のための「分解的手法」と「合成的手法」について,特に,その差異について十分な理解がなされていないのではないかと思うからです.
そもそも,分解的手法とはコッドのリレーショナルデータモデルとその正規化理論に基づく RDB の設計手法で,FD や多値従属性や結合従属性によるリレーションの情報無損失分解がすべてを取り仕切ります.その時,FD が保存されるか否かは,情報無損失分解とは独立した概念であり,本稿で示したように,FD が保存される場合もあれば,保存されない場合もあるわけです.
一方,バーンシュタイン(P.A. Bernstein)により提案された RDB 設計の「合成的手法」[5] は,データベース化の対象となった実世界で成り立つ FD をリストアップし,それを所与の FD 集合と指定することで,それから「関数従属性保存・3NF・情報無損失分解」と三拍子そろった RDB を設計することができます.
つまり,3NF のリレーションスキーマを設計するにあたり,分解的手法では情報無損失分解と関数従属性保存はセットではありませんが,合成的手法では情報無損失分解と関数従属性保存はセットです.ここで,セットという言葉は共に成り立つ,という意味で使っています.これはとても大きな違いなのですが,このことがひょっとして RDB 設計の現場で十分認識されないまま,いつしか分解的手法でも 3NF までならば「関数従属性保存・3NF・情報無損失分解」と三拍子そろった RDB を設計することができるやに誤認識されて今日に至っているのではないか,筆者はそれをとても危惧してこの記事を書いたということです.本稿をお読みいただいた方の中には RDB 設計の最前線に立たれている方も大勢いらっしゃるのではないかと思いますが,機会があれば現場の声を是非お聞かせ願いたく思います.
【文献】
[1]
|
平成26年度春期データベーススペシャリスト試験午前Ⅱ問題 https://www.jitec.ipa.go.jp/1_04hanni_sukiru/mondai_kaitou_2014h26_1/2014h26h_db_am2_qs.pdf |
[2]
|
平成26年度春期データベーススペシャリスト試験解答例 https://www.jitec.ipa.go.jp/1_04hanni_sukiru/mondai_kaitou_2014h26_1/2014h26h_db_am2_ans.pdf |
[3]
| E.F. Codd. A Relational Model of Data for Large Shared Data Banks. Communications of the ACM, Vol.13, No.6, pp.377-387, 1970. |
[4]
| E.F. Codd. Further Normalization of the Data Base Relational Model. R. Rustin (Ed.), Data Base Systems (Courant Computer Science Symposia 6), pp.33-64, Prentice-Hall, Englewood Cliffs, NJ, 1972. |
[5]
| P.A. Bernstein. Synthesizing Third Normal Form Relations from Functional Dependencies. ACM Transactions on Database Systems, Vol.1, No.4, pp.277-298, 1976. |
[6]
| 増永良文.リレーショナルデータベース入門[第3版].サイエンス社,2017. |